In ∆ABC and ∆PQR, in a one to one correspondence \[\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}\]
Problem Set 1 | Q 1.1 | Page 26
Select the appropriate alternative.
In ∆ABC and ∆PQR, in a one to one correspondence
\[\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}\]
(A) D PQR ~ D ABC
(B) D PQR ~ D CAB
(C) D CBA ~ D PQR
(D) D BCA ~ D PQR
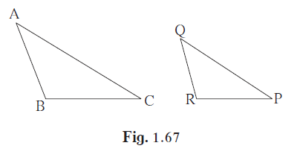
\[\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}\]
By SSS test of similarity
∆PQR ~ ∆CAB
Hence, the correct option is ∆PQR ~ ∆CAB.
Answer:-
The correct option is: ∆PQR ~ ∆CAB.
Explanation: The given ratios indicate that the corresponding sides of the two triangles are proportional. However, we cannot conclude that the triangles are similar based on this information alone. To show that two triangles are similar, we need to show that their corresponding angles are equal or that the ratios of their corresponding sides are equal.
In this case, we can use the SSS (Side-Side-Side) test of similarity to show that ∆PQR is similar to ∆CAB. This test states that if the lengths of the corresponding sides of two triangles are proportional, then the triangles are similar.
Therefore, we can conclude that ∆PQR ~ ∆CAB.
Problem Set 1 | Q 1.1 | Page 26
Click Here for All Textbook Soutions of Chapter 1: Similarity
