In the given figure, if AB || CD || FE then Find x and AE.  

In the given figure, if AB || CD || FE then Find x and AE.

Practice Set 1.2 | Q 7 | Page 14
In the given figure, if AB || CD || FE then Find x and AE.  

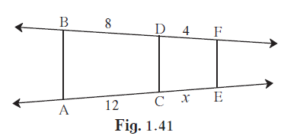
In figure 1.41, if AB || CD || FE then find x and AE.
Solution

In △ABF, DX || AB 

[frac{text{FD}}{text{DB}} = frac{text{FX}}{text{XA}} . . . left( 1 right) left( text{ By Basic proportionality theorem } right)] 

In △AEF, XC || FE 

[frac{text{FX}}{text{XA}} = frac{text{EC}}{text{CA}} . . . left( 2 right) left( text{ By Basic proportionality theorem } right)]

from (1) and (2) , we get 

[frac{text{FD}}{text{DB}} = frac{text{EC}}{text{CA}}]

[ Rightarrow frac{4}{8} = frac{x}{12}]

[ Rightarrow x = 6] 

Now, AE = AC + CE
= 12 + 6
= 18

Solution:-

Here are the steps to find x and AE using the given information in the figure:

  1. Apply the Basic Proportionality Theorem in △ ABF: FD/DB = FX/XA ….(1)

  2. Apply the Basic Proportionality Theorem in △ AEF: FX/XA = EC/CA ….(2)

  3. Equate the right-hand sides of (1) and (2) since FX/XA is common: FD/DB = EC/CA

  4. Substitute the given values: 4/8 = x/12

  5. Simplify the equation: 4 * 12 = 8 * x x = 6

  6. Find AE by adding AC and CE: AE = AC + CE AE = 12 + 6 AE = 18

Therefore, x is equal to 6 and AE is equal to 18 units.

Chapter 1. Similarity- Practice Set 1.2  – Page 13


Q 6


Q 7


Q 8

Click Here for All Textbook Soutions of Chapter 1: Similarity