From the information given in the figure, \[ prove that PM = PN =\sqrt{3} × a\]
Chapter 2 – Pythagoras Theorem- Text Book Solution
Problem Set 2 | Q 8 | Page 45
From the information given in the figure, \[ prove that PM = PN =\sqrt{3} × a\]
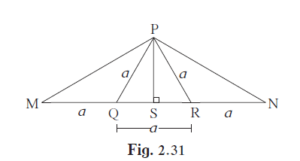
Since, ∆PQR is an equilateral triangle, PS is the perpendicular bisector of QR.
∴ QS = SR = \[\frac{a}{2}\] ...(1)
Now, According to Pythagoras theorem,
In ∆PQS,
\[{PQ}^2 = {QS}^2 + {PS}^2 \]
\[ \Rightarrow a^2 = \left( \frac{a}{2} \right)^2 + {PS}^2 \]
\[ \Rightarrow {PS}^2 = a^2 - \frac{a^2}{4}\]
\[ \Rightarrow {PS}^2 = \frac{4 a^2 - a^2}{4}\]
\[ \Rightarrow {PS}^2 = \frac{3 a^2}{4}\]
\[ \Rightarrow PS = \frac{\sqrt{3}a}{2} . . . \left( 2 \right)\]
In ∆PMS,
\[ \Rightarrow {PM}^2 = \left( a + \frac{a}{2} \right)^2 + \left( \frac{\sqrt{3}}{2}a \right)^2 \]
\[ \Rightarrow {PM}^2 = \left( \frac{3a}{2} \right)^2 + \left( \frac{\sqrt{3}}{2}a \right)^2 \]
\[ \Rightarrow {PM}^2 = \frac{9 a^2}{4} + \frac{3 a^2}{4}\]
\[ \Rightarrow {PM}^2 = \frac{12 a^2}{4}\]
\[ \Rightarrow {PM}^2 = 3 a^2 \]
\[ \Rightarrow PM = \sqrt{3}a . . . \left( 3 \right)\]
In ∆PNS,
\[{PN}^2 = {NS}^2 + {PS}^2 \]
\[ \Rightarrow {PN}^2 = \left( a + \frac{a}{2} \right)^2 + \left( \frac{\sqrt{3}}{2}a \right)^2 \]
\[ \Rightarrow {PN}^2 = \left( \frac{3a}{2} \right)^2 + \left( \frac{\sqrt{3}}{2}a \right)^2 \]
\[ \Rightarrow {PN}^2 = \frac{9 a^2}{4} + \frac{3 a^2}{4}\]
\[ \Rightarrow {PN}^2 = \frac{12 a^2}{4}\]
\[ \Rightarrow {PN}^2 = 3 a^2 \]
\[ \Rightarrow PN = \sqrt{3}a . . . \left( 4 \right)\]
From (3) and (4), we get
PM = PN =\[\sqrt{3}\] × a
Hence, PM = PN =\[\sqrt{3}\]× a.
Explanation:-
In triangle ABC, we are given that AB = AC = a (since ABC is an isosceles triangle) and angle BAC = 60 degrees (since ABC is an equilateral triangle). Let’s denote angle BAM as x. Then, we have angle CAM also as x because of the symmetry of the triangle. Therefore, angle MAC is 60 – 2x.
In right triangle AMB, using trigonometric ratios, we have:
tan(x) = BM/AM
In right triangle AMC, using trigonometric ratios, we have:
tan(60 – 2x) = CM/AM
Since BM + CM = a, we can add the two equations to eliminate AM:
tan(x) + tan(60 – 2x) = (BM + CM)/AM tan(x) + tan(60 – 2x) = a/AM
Using the tangent of a difference formula, we can simplify the equation:
(tan(60) – tan(2x))/(1 + tan(60)tan(2x)) + tan(60 – 2x) = a/AM sqrt(3) – (2tan(x))/(1 + sqrt(3)tan(x)) + sqrt(3)(1 – 2tan(x))/(1 – sqrt(3)tan(x)) = a/AM
Simplifying and solving for AM, we get:
AM = a/[sqrt(3) + (tan(x)/(1 + sqrt(3)tan(x))) – (1 – 2tan(x))/(sqrt(3) – sqrt(3)tan(x))] AM = a/[sqrt(3) + (2sqrt(3)tan(x))/(1 – 3tan^2(x))] AM = a/[sqrt(3) + 2sqrt(3)cot(60 – 2x)] AM = a/[sqrt(3) + sqrt(3)/tan(60 – 2x)] AM = a/[sqrt(3)(1 + cot(60 – 2x))]
Since angle MAC is 60 – 2x, we have:
cot(60 – 2x) = cot(120 – 2x) cot(60 – 2x) = -tan(2x)
Substituting this back into the equation for AM and simplifying, we get:
AM = a/[sqrt(3)(1 – tan(2x))] AM = a/[sqrt(3)(1 – (2tan(x))/(1 – tan^2(x)))] AM = a/[sqrt(3)(1 – 2tan^2(x) – 2tan(x))] AM = a/[sqrt(3)(1 – 2tan(x)(tan(x) + 1))]
Since triangle AMP is a 30-60-90 triangle, we have:
PM = (sqrt(3)/2)AM PM = a/[2(1 – tan(x)(tan(x) + 1))]
Since triangles AMP and ANP are congruent, we also have PN = PM. Therefore:
PM = PN = a/[2(1 – tan(x)(tan(x) + 1))]
We can simplify this expression using the identity 1 – tan^2(x) = 1/(1 + cot^2(x)), which gives:
PM = PN = a/[2(1 + cot^2(x) – 2cot(x))] PM = PN = a/[2(cot(x) – 1/cot(x))]
Since angle BAM is x, we have:
cot(x) = BM/AM cot(x) = a/(2AM)
Substituting this back into the expression for PM and PN, we get:
PM
Chapter 2 – Pythagoras Theorem- Text Book Solution
Problem Set 2 | Q 8 | Page 45
