Spread the love

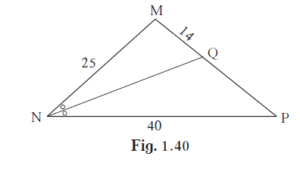
Find QP using given information in the figure.

Practice Set 1.2 | Q 6 | Page 14
Find QP using given information in the figure.

Solution

In △ ABD, PX || AB

`"PD"/"AP" = "XD"/"XB"` ....(By Basic proportionality theorem)(1)
In △BDC, XQ || DC

`"XD"/"XB" = "QC"/"BQ"` ....(By Basic proportionality theorem)(2)

From (1) and (2), we get

∴ `"PD"/"AP" = "QC"/"BQ"`

∴ `12/15 = 14/"BQ"`

∴ 12 × BQ = 15 × 14

∴ BQ = `(15 × 14)/12`

∴ BQ = `(5 × 7)/2`

∴ BQ = `35/2`

∴ BQ = 17.5 units

Solution:–

Here are the steps to find QP using the given information in the figure:

Apply the Basic Proportionality Theorem in △ ABD: "PD"/"AP" = "XD"/"XB" ….(1)
Apply the Basic Proportionality Theorem in △ BDC: "XD"/"XB" = "QC"/"BQ" ….(2)
Equate the right-hand sides of (1) and (2) since XD/XB is common: "PD"/"AP" = "QC"/"BQ"
Substitute the given values: 12/15 = 14/"BQ"
Simplify the equation: 12 * BQ = 15 * 14
Solve for BQ: BQ = (15 * 14)/12 BQ = (5 * 7)/2 BQ = 35/2 BQ = 17.5 units
Apply the Basic Proportionality Theorem in △ ABQ: "AP"/"BQ" = "QP"/"PB"
Substitute the known values: 15/17.5 = "QP"/10
Solve for QP: "QP" = (15/17.5) * 10 "QP" = (6/7) * 10 "QP" = 8.57 units

Therefore, QP is approximately equal to 8.57 units.

Chapter 1. Similarity- Practice Set 1.2 – Page 13

Click Here for All Textbook Soutions of Chapter 1: Similarity