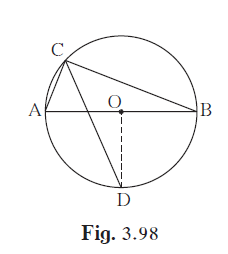
In the given figure, seg AB is a diameter of a circle with centre O.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 20 | Page 89
In the given figure, seg AB is a diameter of a circle with centre O. The bisector of ∠ACB intersects the circle at point D. Prove that, seg AD ≅ seg BD.
Complete the following proof by filling in the blanks.
Proof: Draw seg OD.
∠ACB = ______ …(Angle inscribed in semicircle)
∠DCB = ______ …(CD is the bisector of ∠C)
m(arc DB) = ______ …(Inscribed angle theorem)
∠DOB = ______ …(Definition of measure of an arc)(I)
seg OA ≅ seg OB …( ____________ )(II)
∴ line OD is ______ of seg AB. …[From (I) and (II)]
∴ seg AD ≅ seg BD.
Proof: Draw seg OD.
∠ACB = 90° ...(Angle inscribed in semicircle)
∠DCB = 45° ...(CD is the bisector of ∠C)
m(arc DB) = 2∠DCB = 90° ...(Inscribed angle theorem)
∠DOB = 90° ...(Definition of measure of an arc)(I)
seg OA ≅ seg OB ...( Radii of the circle )(II)
∴ line OD is perpendicular bisector of seg AB. ...[From (I) and (II)]
∴ seg AD ≅ seg BD
Explanation:-
To prove that segment AD is congruent to segment BD, the following steps are taken:
- Draw segment OD, where O is the center of the circle and D is a point on the circle.
- Using the properties of angles inscribed in a semicircle, it is known that angle ACB is 90 degrees.
- Since CD is the bisector of angle C, angle DCB is 45 degrees.
- Using the inscribed angle theorem, it can be shown that the measure of arc DB is twice angle DCB, which equals 90 degrees.
- By the definition of the measure of an arc, angle DOB is 90 degrees.
- Using the fact that OA and OB are radii of the circle and therefore congruent, it can be shown that line OD is the perpendicular bisector of segment AB.
- Therefore, segments AD and BD are congruent by the perpendicular bisector theorem.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 20 | Page 89
Click Here to see All the Textbook solution of Circle
