Find QP using given information in the figure.
Practice Set 1.2 | Q 6 | Page 14
Find QP using given information in the figure.
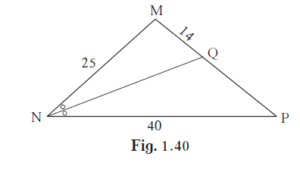
In △ ABD, PX || AB
`"PD"/"AP" = "XD"/"XB"` ....(By Basic proportionality theorem)(1)
In △BDC, XQ || DC
`"XD"/"XB" = "QC"/"BQ"` ....(By Basic proportionality theorem)(2)
From (1) and (2), we get
∴ `"PD"/"AP" = "QC"/"BQ"`
∴ `12/15 = 14/"BQ"`
∴ 12 × BQ = 15 × 14
∴ BQ = `(15 × 14)/12`
∴ BQ = `(5 × 7)/2`
∴ BQ = `35/2`
∴ BQ = 17.5 units
Solution:–
Here are the steps to find QP using the given information in the figure:
Apply the Basic Proportionality Theorem in △ ABD:
"PD"/"AP" = "XD"/"XB"….(1)Apply the Basic Proportionality Theorem in △ BDC:
"XD"/"XB" = "QC"/"BQ"….(2)Equate the right-hand sides of (1) and (2) since XD/XB is common:
"PD"/"AP" = "QC"/"BQ"Substitute the given values:
12/15 = 14/"BQ"Simplify the equation:
12 * BQ = 15 * 14Solve for BQ:
BQ = (15 * 14)/12BQ = (5 * 7)/2BQ = 35/2BQ = 17.5 unitsApply the Basic Proportionality Theorem in △ ABQ:
"AP"/"BQ" = "QP"/"PB"Substitute the known values:
15/17.5 = "QP"/10Solve for QP:
"QP" = (15/17.5) * 10"QP" = (6/7) * 10"QP" = 8.57 units
Therefore, QP is approximately equal to 8.57 units.
Chapter 1. Similarity- Practice Set 1.2 – Page 13
Click Here for All Textbook Soutions of Chapter 1: Similarity
