In the given figure, points G, D, E, F are concyclic points of a circle with centre C. ∠ ECF = 70°, m(arc DGF) = 200° find m(arc DE) and m(arc DEF).
Chapter 3 – Circle – Text Book Solution
Practice Set 3.3 | Q 1 | Page 63
In the given figure, points G, D, E, F are concyclic points of a circle with centre C.
∠ ECF = 70°, m(arc DGF) = 200° find m(arc DE) and m(arc DEF).
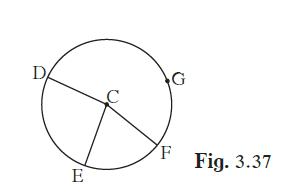
m(arc EF) = ∠ECF = 70º (Measure of an arc is the measure of its central angle)
Now,
m(arc DE) = 360º − m(arc EF) − m(arc DGF)
⇒ m(arc DE) = 360º − 70º − 200º = 90º
Also,
m(arc DEF) = m(arc DE) + m(arc EF)
⇒ m(arc DEF) = 90º + 70º = 160º
Thus, the m(arc DE) and m(arc DEF) is 90º and 160º, respectively.
Explanation:–
Given that m(arc EF) = ∠ECF = 70°.
To find m(arc DE), we can use the fact that the sum of the measures of the three arcs that intersect at a point on a circle is 360°. Therefore,
m(arc DE) = 360° – m(arc EF) – m(arc DGF)
Substituting the value of m(arc EF) = 70° and m(arc DGF) = 200° (since it is given that ∠DGF = 200°), we get:
m(arc DE) = 360° – 70° – 200° = 90°
Next, we are asked to find m(arc DEF). We know that m(arc DEF) = m(arc DE) + m(arc EF), so substituting the values of m(arc DE) = 90° and m(arc EF) = 70°, we get:
m(arc DEF) = 90° + 70° = 160°
Thus, we have found that m(arc DE) = 90° and m(arc DEF) = 160°.
Chapter 3 – Circle – Text Book Solution
Practice set 3.3 | Q 1 | Page 63
Click Here to see All the Textbook solution of Circle
