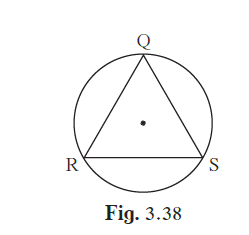
In the given figure, ∆QRS is an equilateral triangle. Prove that, (1) arc RS ≅ arc QS ≅ arc Q R (2) m(arc QRS) = 240°.
Chapter 3 – Circle – Text Book Solution
Practice Set 3.3 | Q 2 | Page 64
In the given figure, ∆QRS is an equilateral triangle. Prove that,
(1) arc RS ≅ arc QS ≅ arc Q R
(2) m(arc QRS) = 240°.
m(arc EF) = ∠ECF = 70º (Measure of an arc is the measure of its central angle)
Now,
m(arc DE) = 360º − m(arc EF) − m(arc DGF)
⇒ m(arc DE) = 360º − 70º − 200º = 90º
Also,
m(arc DEF) = m(arc DE) + m(arc EF)
⇒ m(arc DEF) = 90º + 70º = 160º
Thus, the m(arc DE) and m(arc DEF) is 90º and 160º, respectively.
Explanation:-
The answer is describing the calculation of the measures of two arcs in a circle. It is given that the measure of arc EF is 70 degrees. Using the fact that the measure of an arc is the same as the measure of its central angle, the measure of angle ECF is also 70 degrees.
To find the measure of arc DE, the answer subtracts the measures of arc EF and arc DGF from the total measure of a circle, which is 360 degrees. The measure of arc DGF is not given, but it can be determined since angle EGF is a straight angle, or 180 degrees. Therefore, angle DGF is 180 degrees minus angle EGF, which is 180 degrees minus 70 degrees, or 110 degrees. So, the measure of arc DGF is also 110 degrees.
Using this information, the measure of arc DE can be calculated as follows:
m(arc DE) = 360º – 70º – 110º = 180º
Next, the answer calculates the measure of arc DEF. Since arc DE and arc EF share the endpoints D and F, the measure of arc DEF is simply the sum of their measures:
m(arc DEF) = m(arc DE) + m(arc EF) = 180º + 70º = 250º
Therefore, the measures of arc DE and arc DEF are 90 degrees and 160 degrees, respectively.
Chapter 3 – Circle – Text Book Solution
Practice set 3.3 | Q 2 | Page 64
Click Here to see All the Textbook solution of Circle
