In the given figure, the circles with centres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD if the radii of the circles are 4 cm, 6 cm.
Chapter 3 – Circle – Text Book Solution
Practice Set 3.2 | Q 5 | Page 58
In the given figure, the circles with centres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD if the radii of the circles are 4 cm, 6 cm.
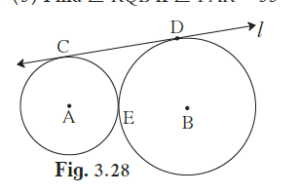
If two circles touch each other externally, then distance between their centres is equal to the sum of their radii.
∴ AB = AE + EB = 4 cm + 6 cm = 10 cm
It is given that l is a common tangent which touches the circles at C and D.
∴ ∠ACD = ∠BDC = 90º (Tangent at any point of a circle is perpendicular to the radius throught the point of contact)
Draw AF ⊥ BD.
Here, ACDF is a rectangle.
∴ CD = AF and DF = AC (Opposite sides of rectangle are equal)
BF = BD − DF = BD − AC = 6 cm − 4 cm = 2 cm
In right ∆ABF,
\[{AB}^2 = {AF}^2 + {BF}^2 \]
\[ \Rightarrow AF = \sqrt{{AB}^2 - {BF}^2} \]
\[ \Rightarrow AF = \sqrt{{10}^2 - 2^2}\]
\[ \Rightarrow AF = \sqrt{100 - 4} = \sqrt{96} = 4\sqrt{6} cm\]
∴ CD = AF = \[4\sqrt{6}\]
Thus, the length of seg CD is \[4\sqrt{6}\]
Explanation:-
Given two circles that touch each other externally, we know that the distance between their centers is equal to the sum of their radii. We can use this fact to solve the problem as follows:
Let the centers of the two circles be A and B, with radii 4 cm and 6 cm, respectively. Let l be a common tangent to the circles, touching them at points C and D. Draw a line segment AF perpendicular to BD, where F is the point of intersection of l and BD.
Since l is tangent to both circles, we have [\angle ACD = \angle BDC = 90^\circ] by the tangent-radius theorem.
Since ACDF is a rectangle, we have CD = AF and DF = AC by the properties of a rectangle.
We can find BF by subtracting DF from BD: BF = BD – DF = 6 cm – 4 cm = 2 cm.
Using the Pythagorean theorem in right triangle ABF, we have [{AB}^2 = {AF}^2 + {BF}^2 ] which implies [AF = \sqrt{{AB}^2 – {BF}^2} = \sqrt{{10}^2 – 2^2} = \sqrt{96} = 4\sqrt{6} \text{ cm}].
Therefore, CD = AF = [4\sqrt{6}] cm.
Explanation:-
Chapter 3 – Circle – Text Book Solution
Practice set 3.2 | Q 5 | Page 58
Click Here to see All the Textbook solution of Circle
