In the adjoining figure, O is the centre of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm
Chapter 3 – CIrcle- Text Book Solution
Practice Set 3.1 | Q 2 | Page 55
In the adjoining figure, O is the centre of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then
(1) What is the length of each tangent segment ?
(2) What is the measure of ∠MRO ?
(3) What is the measure of ∠ MRN ?
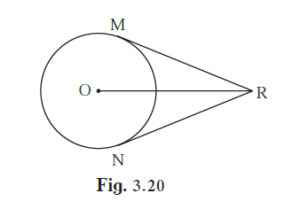
(1) It is given that seg RM and seg RN are tangent segments touching the circle at M and N, respectively.
∴ ∠OMR = ∠ONR = 90º (Tangent at any point of a circle is perpendicular to the radius throught the point of contact)
OM = 5 cm and OR = 10 cm
In right ∆OMR,
\[{OR}^2 = {OM}^2 + {MR}^2 \]
\[ \Rightarrow MR = \sqrt{{OR}^2 - {OM}^2} \]
\[ \Rightarrow MR = \sqrt{{10}^2 - 5^2}\]
\[ \Rightarrow MR = \sqrt{100 - 25} = \sqrt{75} = 5\sqrt{3} cm\]
Tangent segments drawn from an external point to a circle are congruent.
∴ MR = NR =\[5\sqrt{3}\]
(2) In right ∆OMR,
\[\tan\angle MRO = \frac{OM}{MR}\]
\[ \Rightarrow \tan\angle MRO = \frac{5 cm}{5\sqrt{3} cm} = \frac{1}{\sqrt{3}}\]
\[ \Rightarrow \tan\angle MRO = \tan30^\circ\]
\[ \Rightarrow \angle MRO = 30^\circ\]
Thus, the measure of ∠MRO is 30º.
Similarly, ∠NRO = 30º
(3) ∠MRN = ∠MRO + ∠NRO = 30º + 30º = 60º
Thus, the measure of ∠MRN is 60º.
Explanation:-
- Segments RM and RN are tangent to the circle at points M and N, respectively, which means that angles OMR and ONR are both right angles, as the tangent at any point of a circle is perpendicular to the radius through the point of contact.
We also know that OM is 5 cm and OR is 10 cm. By using the Pythagorean theorem in right triangle OMR, we can find that MR is equal to 5√3 cm.
Tangent segments drawn from an external point to a circle are congruent, so MR = NR = 5√3 cm.
In right triangle OMR, we can use the tangent function to find the measure of angle MRO. By dividing OM by MR, we get 1/√3, which is equal to tan30°. Therefore, angle MRO measures 30°. We can use the same method to find that angle NRO also measures 30°.
Angle MRN is equal to the sum of angles MRO and NRO, which is 30° + 30° = 60°. Therefore, the measure of angle MRN is 60°.
Chapter 3 – Circle – Text Book Solution
Practice set 3.1 | Q 2 | Page 55
Click Here to see All the Textbook solution of Circle
