Line l touches a circle with centre O at point P. If radius of the circle is 9 cm,
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 2 | Page 84
Line l touches a circle with centre O at point P. If radius of the circle is 9 cm, answer the following.
(1) What is d(O, P) = ? Why ?
(2) If d(O, Q) = 8 cm, where does the point Q lie ?
(3) If d(OQ) = 15 cm, How many locations of point Q are line on line l? At what distance will each of them be from point P?
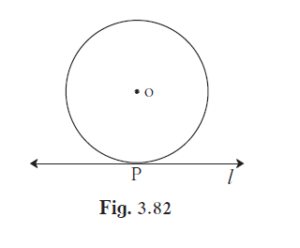
Radius of the circle = 9 cm
(1) It is given that line l is tangent to the circle at P.
∴ OP = 9 cm ...(Radius of the circle)
d(O, P) = 9 cm
(2) d(O, Q) = 8 cm < Radius of the circle
∴ Point Q lies in the interior of the circle.
(3) If d(OQ) = 15 cm, then there are two locations of point Q on the line l. One on the left of point P and one on the right of point P.
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ ∠OPQ = 90º
In right ∆OPQ,
OQ2 = OP2 + PQ2
PQ = `sqrt("OQ"^2 - "OP"^2)`
PQ = `sqrt(15^2 - 9^2)`
PQ = `sqrt(225 - 81)`
PQ = `sqrt(144)`
PQ = 12 cm
Thus, the two locations of the point Q on line l, which are at a distance of 12 cm from point P.
Explanation:-
Consider a circle with radius 9 cm.
(1) Given that line l is tangent to the circle at point P.
Since P is the point of contact between line l and the circle, OP is perpendicular to line l. Therefore, OP is the radius of the circle and its length is 9 cm.
Also, d(O,P) represents the distance between point O (the center of the circle) and point P. Since P lies on the circle, the distance between O and P is equal to the radius of the circle, which is 9 cm.
(2) Given that d(O,Q) = 8 cm < radius of the circle.
Since the distance between O and Q is less than the radius of the circle, point Q lies inside the circle.
(3) Given that if d(OQ) = 15 cm, then there are two locations of point Q on the line l, one on the left of point P and one on the right of point P.
Since line l is tangent to the circle at point P, the radius OP is perpendicular to line l. Therefore, angle OPQ is a right angle (90°).
In right triangle OPQ, using the Pythagorean theorem, we have:
OQ^2 = OP^2 + PQ^2
where PQ represents the distance between points P and Q.
Solving for PQ, we get:
PQ = sqrt(OQ^2 – OP^2)
Substituting OQ = 15 cm and OP = 9 cm, we get:
PQ = sqrt(15^2 – 9^2) = sqrt(144) = 12 cm
Therefore, the two locations of point Q on line l are at a distance of 12 cm from point P.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 2 | Page 84
Click Here to see All the Textbook solution of Circle
