In ∆ABC and ∆DEF ∠B = ∠E, ∠F = ∠C and AB = 3DE then which of the statements regarding the two triangles is true ?
Problem Set 1 | Q 1.3 | Page 26
In ∆ABC and ∆DEF ∠B = ∠E, ∠F = ∠C and AB = 3DE then which of the statements regarding the two triangles is true ?
The triangles are not congruent and not similar
The triangles are similar but not congruent.
The triangles are congruent and similar.
None of the statements above is true.
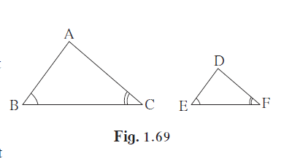
In ∆ABC and ∆DEF
∠B = ∠E,
∠F = ∠C
By AA test of similarity
∆ABC ~ ∆DEF
Since, there is not any congruency criteria like AA.
Thus, ∆ABC and ∆DEF are not congruent.
Hence, the correct option is The triangles are similar but not congruent.
Solution:-
Based on the given information:
∠B = ∠E
∠F = ∠C
AB = 3DE
We cannot conclude that the triangles are congruent because we do not have enough information about the length of the sides or other angles.
However, we can use the Angle-Angle (AA) similarity criterion to show that the triangles are similar.
∠B = ∠E and ∠C = ∠F, so ∆ABC ~ ∆DEF by AA similarity.
Therefore, the correct statement is: The triangles are similar but not congruent.
So, option 2 is the correct answer.
Problem Set 1 | Q 1.3 | Page 26
Click Here for All Textbook Soutions of Chapter 1: Similarity
