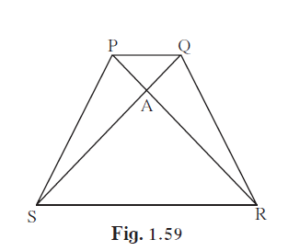
In trapezium PQRS, side PQ || side SR, AR = 5AP, AS = 5AQ then prove that, SR = 5PQ
Practice Set 1.3 | Q 5 | Page 22
In trapezium PQRS, side PQ || side SR, AR = 5AP, AS = 5AQ then prove that, SR = 5PQ
Solution
Given:
side PQ || side SR
AR = 5AP,
AS = 5AQ
To prove: SR = 5PQ
Proof: In ∆APQ and ∆ARS
∠PAQ = ∠RAS (Vertically Opposite angles)
∠PQA = ∠RSA (Alternate angles, side PQ || side SR and QS is a transversal line)
By AA test of similarity
∆APQ ~ ∆ARS
[frac{PQ}{SR} = frac{AP}{AR} left( text{ Corresponding sides are proportional } right)]
[ Rightarrow frac{PQ}{SR} = frac{1}{5} left( AR = 5AP right)]
[ Rightarrow SR = 5PQ]
Hence proved.
Given:
- PQ || SR
- AR = 5AP
- AS = 5AQ
To prove: SR = 5PQ
Proof:
-
In ∆APQ and ∆ARS, we have:
- ∠PAQ = ∠RAS (Vertically Opposite angles)
- ∠PQA = ∠RSA (Alternate angles, PQ || SR and QS is a transversal line)
- By AA test of similarity, we have ∆APQ ~ ∆ARS
-
Therefore, we can write:
- PQ/SR = AP/AR (Corresponding sides are proportional)
- PQ/SR = 1/5 (AR = 5AP)
- SR = 5PQ
Hence, we have proved that SR = 5PQ.
Chapter 1. Similarity- Practice Set 1.3 – Page 22
Click Here for All Textbook Soutions of Chapter 1: Similarity