In the given figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠ RTS is an acute angle.
Chapter 3 – Circle – Text Book Solution
Practice Set 3.4 | Q 4 | Page 73
In the given figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠ RTS is an acute angle.
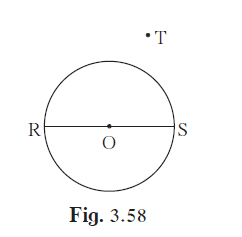
Join RT and TS. Suppose RT intersect the circle at P.
It is given that seg RS is a diameter of the circle with centre O.
∴ ∠RPS = 90º (Angle in a semi-circle is 90º)
In ∆PTS, ∠RPS is an exterior angle and ∠PTS is its remote interior angle.
We know, an exterior angle of a triangle is greater than its remote interior angle.
∴ ∠RPS > ∠PTS
⇒ 90º > ∠PTS
Or ∠RTS < 90º (∠PTS = ∠RTS)
Thus, ∠RTS is an acute angle.
Explanation:-
Join the line segments RT and TS. Suppose RT intersects the circle at point P.
It is given that the line segment RS is a diameter of the circle with center O. Therefore, angle RPS is a right angle (90 degrees) since it is an angle in a semicircle (by Thales’ theorem).
Consider triangle PTS. Angle RPS is an exterior angle of this triangle and angle PTS is its remote interior angle. It is a known property that the measure of an exterior angle of a triangle is greater than the measure of its remote interior angle.
Therefore, angle RPS is greater than angle PTS: RPS > PTS. Thus, we have:
90 degrees > PTS
Since angle PTS is equal to angle RTS (both subtend the same arc), it follows that angle RTS is less than 90 degrees: RTS < 90 degrees.
Thus, angle RTS is an acute angle.
Chapter 3 – Circle – Text Book Solution
Practice set 3.4 | Q 4 | Page 73
Click Here to see All the Textbook solution of Circle
