In the given figure, PM = 10 cm A(∆PQS) = 100 sq.cm A(∆QRS) = 110 sq.cm then Find NR.
Problem Set 1 | Q 5 | Page 27
In the given figure, PM = 10 cm A(∆PQS) = 100 sq.cm A(∆QRS) = 110 sq.cm then Find NR.
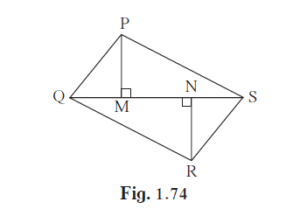
Given:
PM = 10 cm
A(∆PQS) = 100 sq.cm
A(∆QRS) = 110 sq.cm
\[\text{ Now }, \frac{A \left( ∆ PQS \right)}{A \left( ∆ QRS \right)} = \frac{100}{110}\]
\[ \Rightarrow \frac{\frac{1}{2} \times PM \times QS}{\frac{1}{2} \times RN \times QS} = \frac{10}{11}\]
\[\Rightarrow \frac{10}{RN} = \frac{10}{11}\]
\[ \Rightarrow RN = 11\] cm
Answer:_ Given:
PM = 10 cm Area of triangle PQS = 100 sq.cm Area of triangle QRS = 110 sq.cm
Step 1: Use the formula for the ratio of the areas of two similar triangles The problem tells us that the triangles PQS and QRS are similar. We can use the formula for the ratio of the areas of two similar triangles:
A(∆PQS) / A(∆QRS) = (PQ/QR)^2
Step 2: Plug in the given values We know that the areas are 100 and 110, respectively:
100 / 110 = (PQ/QR)^2
Simplifying:
10 / 11 = PQ/QR
Step 3: Use the formula for the area of a triangle The area of a triangle is equal to half the product of the base and the height:
A = 1/2 * base * height
We can use this formula to write the ratios of the bases and heights of the triangles:
A(∆PQS) / A(∆QRS) = (PQ/QR)^2 1/2 * PM * QS / 1/2 * RN * QS = (PQ/QR)^2
Simplifying:
PM / RN = PQ/QR
Step 4: Plug in the given value of PM and the ratio of PQ/QR We know that PM = 10 cm and PQ/QR = 10/11:
10 / RN = 10/11
Simplifying:
RN = 11 cm
Therefore, the length of the line segment RN is 11 cm.
Problem Set 1 | Q 5 | Page 27
Click Here for All Textbook Soutions of Chapter 1: Similarity
