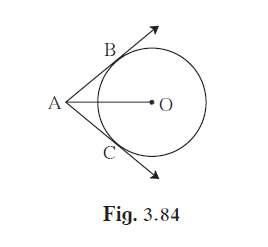
In the given figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB) = r, Prove that ▢ABOC is a square.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 4 | Page 84
In the given figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB) = r, Prove that ▢ABOC is a square.
Proof: Draw segment OB and OC.
l(AB) = r ……[Given] (I)
AB = AC ……[`square`] (II)
But OB = OC = r ……[`square`] (III)
From (i), (ii) and (iii)
AB = `square` = OB = OC = r
∴ Quadrilateral ABOC is `square`
Similarly, ∠OBA = `square` ……[Tangent Theorem]
If one angle of `square` is right angle, then it is a square.
∴ Quadrilateral ABOC is a square.
l(AB) = r ......[Given] (I)
AB = AC ......[`square`] (II)
But OB = OC = r ......[`square`] (III)
From (i), (ii) and (iii)
AB = `square` = OB = OC = r
∴ Quadrilateral ABOC is `square`
Similarly, ∠OBA = `square` ......[Tangent Theorem]
If one angle of `square` is right angle, then it is a square.
∴ Quadrilateral ABOC is a square.
Explanation:-
Given that line AB is tangent to the circle with center O and radius r at point B, i.e., AB = r (given condition I). Also, AB = AC (given condition II), and OB = OC = r (given condition III).
From these conditions, we can see that AB = OB = OC = r. Therefore, the points A, B, O, and C form a square (because all sides are equal and opposite sides are parallel).
Now, we know that angle OBA is a right angle because AB is tangent to the circle at point B (Tangent Theorem). Since one angle of the square is a right angle, all angles of the square are right angles. Therefore, the quadrilateral ABOC is a square.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 4 | Page 84
Click Here to see All the Textbook solution of Circle
