In the given figure, circle with centre M touches the circle with centre N at point T.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 6 | Page 85
In the given figure, circle with centre M touches the circle with centre N at point T. Radius RM touches the smaller circle at S. Radii of circles are 9 cm and 2.5 cm. Find the answers to the following questions hence find the ratio MS:SR.
(1) Find the length of segment MT
(2) Find the length of seg MN
(3) Find the measure of ∠NSM.
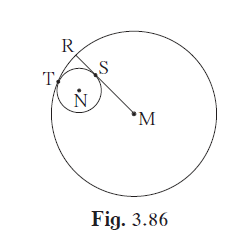
Radius of circle with centre M = 9 cm
Radius of circle with centre N = 2.5 cm
Join MT and NS.
If two circles touch each other, their point of contact lie on the line joining their centres. So, the points M, N and T are collinear.
(1)
Length of segment MT = 9 cm (Radius of circle with centre M)
Thus, the length of the segment MT is 9 cm.
(2)
Length of segment NT = 2.5 cm (Radius of circle with centre N)
∴ Length of segment MN = Length of segment MT − Length of segment NT = 9 − 2.5 = 6.5 cm
Thus, the length of the segment MN is 6.5 cm.
(3)
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
In the given figure, seg RM is tangent to the circle with centre N at point S.
∴ ∠NSM = 90º
In right ∆NSM,
\[{MN}^2 = {NS}^2 + {SM}^2 \]
\[ \Rightarrow SM = \sqrt{{MN}^2 - {NS}^2}\]
\[ \Rightarrow SM = \sqrt{\left( 6 . 5 \right)^2 - \left( 2 . 5 \right)^2}\]
\[ \Rightarrow SM = \sqrt{42 . 25 - 6 . 25}\]
\[ \Rightarrow SM = \sqrt{36} = 6 \] cm
∴ SR = MR − SM = 9 − 6 = 3 cm (MR = Radius of the circle with centre M)
⇒ MS : SR = 6 cm : 3 cm = 2 : 1
Thus, the ratio MS : SR is 2 : 1.
Explanation:-
The problem provides the following information:
- The radius of a circle with centre M is 9 cm.
- The radius of a circle with centre N is 2.5 cm.
- MT and NS are joined.
To find: The ratio of MS:SR.
From the given information, we can determine the following:
- The points M, N and T are collinear as the circles touch each other, and their point of contact lies on the line joining their centres. This can be represented as MNT are collinear.
- The length of segment MT is 9 cm, which is the radius of circle M.
- The length of segment NT is 2.5 cm, which is the radius of circle N.
- The length of segment MN can be calculated as MN = MT – NT = 9 – 2.5 = 6.5 cm.
Using the tangent theorem, we can find the length of SM.
- The tangent at any point of a circle is perpendicular to the radius through the point of contact.
- Segment RM is tangent to the circle with centre N at point S.
- Therefore, ∠NSM = 90°.
- Using the Pythagorean theorem, we can find SM: MN² = NS² + SM².
- Therefore, SM = √(MN² – NS²) = √((6.5)² – (2.5)²) = √(42.25 – 6.25) = √(36) = 6 cm.
Now, we can find the length of SR using the fact that MR = 9 cm.
- SR = MR – SM = 9 – 6 = 3 cm.
Finally, we can find the ratio MS:SR.
- MS:SR = 2:1, as MS is twice the length of SR (MS = 2 x SR = 2 x 3 = 6 cm).
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 6 | Page 85
Click Here to see All the Textbook solution of Circle
