In the given figure, BC ⊥ AB, AD ⊥ AB, BC = 4, AD = 8, then find (A(∆ABC))/(A(∆ADB))
Practice Set 1.1 | Q 2 | Page 6
In the given figure, BC ⊥ AB, AD ⊥ AB, BC = 4, AD = 8, then find (A(∆ABC))/(A(∆ADB))
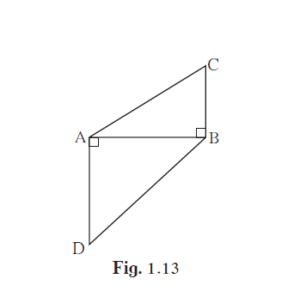
In ∆ABC and ∆ADB,
BC ⊥ AB, AD ⊥ AB, BC = 4, AD = 8 ...(Given)
∆ABC and ∆ADB have same base AB. ...(Given)
∴ Areas of triangles with equal bases are proportional to their corresponding heights.
(A(∆ABC))/(A(∆ADB)) = BC/AD
∴ (A(∆ABC))/(A(∆ADB)) = 4/8
∴ (A(∆ABC))/(A(∆ADB)) = 1/2.
Solution 2:- In the given figure, let’s denote the length of AB by ‘x’. Then, we can use the Pythagorean theorem to find the length of BC and AD:
BC² + AB² = AC² 4² + x² = AC² AC = sqrt(16 + x²)
AD² + AB² = BD² 8² + x² = BD² BD = sqrt(64 + x²)
Now, we can find the areas of triangles ABC and ADB:
A(∆ABC) = (1/2) * AB * BC = (1/2) * x * 4 = 2x
A(∆ADB) = (1/2) * AB * AD = (1/2) * x * 8 = 4x
Therefore, the ratio of the areas of the two triangles is:
A(∆ABC) / A(∆ADB) = (2x) / (4x) = 1/2
So, the ratio of the areas of triangles ABC and ADB is 1:2 or 1/2.
Chapter 1. Similarity- Practice Set 1.1 – Page 5
Click Here for All Textbook Soutions of Chapter 1: Similarity
