In the given figure, altitudes YZ and XT of ∆WXY intersect at P. Prove that, (1) ▢WZPT is cyclic. (2) Points X, Z, T, Y are concyclic
Chapter 3 – Circle – Text Book Solution
Practice Set 3.4 | Q 6 | Page 74
In the given figure, altitudes YZ and XT of ∆WXY intersect at P. Prove that,
(1) ▢WZPT is cyclic.
(2) Points X, Z, T, Y are concyclic
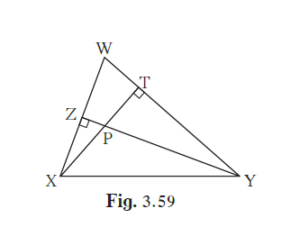
(1) It is given that, YZ ⊥ WX and XT ⊥ WY.
∴ ∠WZY = 90º .....(1)
∠WTX = 90º .....(2)
Adding (1) and (2), we get
∠WZY + ∠WTX = 90º + 90º = 180º
Or ∠WZP + ∠WTP = 90º + 90º = 180º
In quadrilateral WZPT,
∠WZP + ∠WTP = 180º
We know, if a pair of opposite angles of a quadrilateral is supplementary, then quadrilateral is cyclic.
Therefore, quadrilateral WZPT is cyclic.
(2) It is given that, YZ ⊥ WX and XT ⊥ WY.
∴ ∠XZY = 90º and ∠XTY = 90º
⇒ ∠XZY = ∠XTY
So, two points X and Y on the line XY subtends equal angles at two distinct points Z and T which lie on the same side of the line XY.
Therefore, the points X, Z, T and Y are concyclic.
Explanation:-
(1) The problem provides that YZ is perpendicular to WX and XT is perpendicular to WY. Therefore, angles WZY and WTX are both 90 degrees (as given). Adding these angles together gives us WZY + WTX = 90 degrees + 90 degrees = 180 degrees. Therefore, angle WZP + angle WTP = 90 degrees + 90 degrees = 180 degrees. In quadrilateral WZPT, the sum of opposite angles (WZP and WTP) is 180 degrees, which implies that the quadrilateral is cyclic.
(2) The problem also provides that YZ is perpendicular to WX and XT is perpendicular to WY. Therefore, angles XZY and XTY are both 90 degrees (as given). This implies that angle XZY = angle XTY. Therefore, the points X and Y on the line XY subtend equal angles at two distinct points Z and T which lie on the same side of the line XY. Consequently, the points X, Z, T and Y are concyclic.
Chapter 3 – Circle – Text Book Solution
Practice set 3.4 | Q 6 | Page 74
Click Here to see All the Textbook solution of Circle
