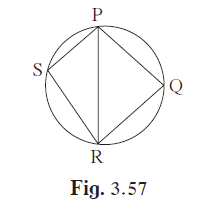
In the given figure, ▢PQRS is cyclic. side PQ ≅ side RQ. ∠PSR = 110°, Find –
(1) measure of ∠PQR
(2) m(arc PQR)
(3) m(arc QR)
(4) measure of ∠PRQ

Chapter 3 – Circle – Text Book Solution

Practice Set 3.4 | Q 2 | Page 73

solution

(1) ▢PQRS is a cyclic quadrilateral. …[Given]

∴ ∠PSR + ∠PQR = 180° …[Opposite angles of a cyclic quadrilateral are supplementary]

∴ 110° + ∠PQR = 180°

∴ ∠PQR = 180° − 110°

∴ m∠PQR = 70°

(2) ∠PSR = `1/2` m(arc PQR) …..[Inscribed angle theorem]

∴ 110° = `1/2` m(arc PQR)

∴ m(arc PQR) = 220°

(3) In ∆PQR,

Side PQ ≅ side RQ …[Given]

∴ ∠PRQ ≅ ∠QPR …[Isosceles triangle theorem]

Let ∠PRQ = ∠QPR = x

Now, ∠PQR + ∠QPR + ∠PRQ = 180° …[Sum of the measures of angles of a triangle is 180°]

∴ ∠PQR + x + x = 180°

∴ 70° + 2x = 180°

∴ 2x = 180° − 70°

∴ 2x = 110°

∴ x = `(110°)/2`

∴ x = 55°

∴ ∠PRQ = ∠QPR = 55° ……(i)

But, ∠QPR = `1/2` m(arc QR) …..[Inscribed angle theorem]

∴ 55° = `1/2` m(arc QR)

∴ m(arc QR) = 110°

(4) In ∆PQR,

∠PQR + ∠PRQ + ∠QPR = 180° …[Sum of the measures of angles of a triangle is 180°]

70° + ∠PRQ + 55° = 180°

∠PRQ = 180° – 125°

∠PRQ = 55°.

Explanation:-

(1) Given that PQRS is a cyclic quadrilateral.

From the opposite angles of a cyclic quadrilateral are supplementary property, we have angle PSR + angle PQR = 180 degrees.
We know that angle PSR is 110 degrees, so angle PQR = 180 – 110 = 70 degrees.

(2) In the quadrilateral PQRS,

The angle PSR is equal to half the measure of the arc PQR.
We know that angle PSR is 110 degrees, so the measure of arc PQR is 2 * 110 = 220 degrees.

(3) In triangle PQR,

PQ is congruent to RQ, which means that the two sides have the same length.
From the isosceles triangle theorem, we have angle PRQ = angle QPR.
Let the measure of angle PRQ (or QPR) be x.
From the sum of the measures of angles of a triangle property, we have angle PQR + angle QPR + angle PRQ = 180 degrees.
We know that angle PQR is 70 degrees, so 70 + 2x = 180.
Solving for x, we get x = 55 degrees.
From the inscribed angle theorem, we know that angle QPR is equal to half the measure of arc QR.
We know that angle QPR is 55 degrees, so the measure of arc QR is 2 * 55 = 110 degrees.

(4) In triangle PQR,

Using the sum of the measures of angles of a triangle property, we have angle PQR + angle PRQ + angle QPR = 180 degrees.
We know that angle PQR is 70 degrees and angle QPR is 55 degrees, so 70 + angle PRQ + 55 = 180.
Solving for angle PRQ, we get angle PRQ = 55 degrees.

Chapter 3 – Circle – Text Book Solution

Practice set 3.4 | Q 2 | Page 73

Q.1

Q 2

Q3

Click Here to see All the Textbook solution of Circle

In the given figure, ▢PQRS is cyclic. side PQ ≅ side RQ. ∠PSR = 110°,