Spread the love

In the given figure, ∠QPR = 90°, seg PM ⊥ seg QR and Q–M–R, PM = 10, QM = 8, find QR

Practice Set 2.1 | Q 3 | Page 38

Solution

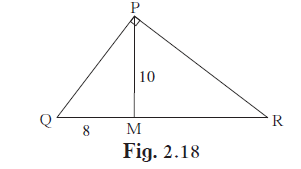
In ΔPQR,

`{:(∠"QPR" = 90°),("seg PM ⊥ seg QR"):} }"Given"`

In a right angled triangle, the perpendicular segment to the hypotenuse from the opposite vertex, is the geometric mean of the segments into which the hypotenuse is divided.

∴ PM² = QM × MR ...(Theorem of geometric mean)

∴ 10² = 8 × MR

∴ 100 = 8 × MR

∴ MR = `100/8`

∴ MR = 12.5

Now,

QR = QM + MR ...(Q-M-R)

∴ QR = 8 + 12.5

∴ QR = 20.5

Explanation:-

We are given a right-angled triangle ΔPQR, where ∠QPR = 90°, and PM is perpendicular to QR.

According to the theorem of geometric mean, in a right-angled triangle, the perpendicular segment to the hypotenuse from the opposite vertex is the geometric mean of the segments into which the hypotenuse is divided.

Therefore, we have:

PM^2 = QM × MR

Substituting the given values, we get:

10^2 = 8 × MR

Simplifying, we get:

100 = 8 × MR

Dividing both sides by 8, we get:

MR = 100/8

Simplifying further, we get:

MR = 12.5

Now, we can use the Pythagorean theorem to find the length of QR, which is the hypotenuse of the right-angled triangle.

We know that:

QR^2 = QM^2 + MR^2

Substituting the given values, we get:

QR^2 = 8^2 + 12.5^2

Simplifying, we get:

QR^2 = 64 + 156.25

QR^2 = 220.25

Taking the square root on both sides, we get:

QR = √220.25

QR = 20.5

Hence, we have found that the length of QR is 20.5 units.

Chapter 2 – Pythagoras Theorem- Text Book Solution

Practice Set 2.1 | Q 3 | Page 38