In the given figure, ∆PQR is an equilateral triangle. Point S is on seg QR
Chapter 2 – Pythagoras Theorem- Text Book Solution
Problem Set 2 | Q 16 | Page 44
In the given figure, ∆PQR is an equilateral triangle. Point S is on seg QR such thatn QS =n\[\frac{1}{3}\] QR
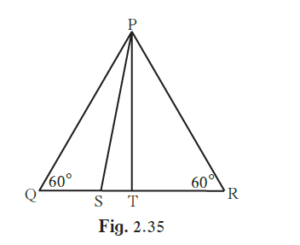
solution
Given: QS =
\[\frac{1}{3}\] QR = \[\frac{x}{3}\]
\[\therefore ST = QT - QS = \frac{x}{2} - \frac{x}{3} = \frac{x}{6}\]
According to Pythagoras theorem,
In ∆PQT
In ∆PQT
\[{PQ}^2 = {QT}^2 + {PT}^2 \]
\[ \Rightarrow \left( x \right)^2 = \left( \frac{x}{2} \right)^2 + {PT}^2 \]
\[ \Rightarrow x^2 = \frac{x^2}{4} + {PT}^2 \]
\[ \Rightarrow {PT}^2 = x^2 - \frac{x^2}{4}\]
\[ \Rightarrow {PT}^2 = \frac{3 x^2}{4}\]
\[ \Rightarrow PT = \frac{\sqrt{3}x}{2}\]
\[ \Rightarrow \left( x \right)^2 = \left( \frac{x}{2} \right)^2 + {PT}^2 \]
\[ \Rightarrow x^2 = \frac{x^2}{4} + {PT}^2 \]
\[ \Rightarrow {PT}^2 = x^2 - \frac{x^2}{4}\]
\[ \Rightarrow {PT}^2 = \frac{3 x^2}{4}\]
\[ \Rightarrow PT = \frac{\sqrt{3}x}{2}\]
In ∆PST
\[{PS}^2 = {ST}^2 + {PT}^2 \]
\[ \Rightarrow {PS}^2 = \left( \frac{x}{6} \right)^2 + \left( \frac{\sqrt{3}x}{2} \right)^2 \]
\[ \Rightarrow {PS}^2 = \frac{x^2}{36} + \frac{3 x^2}{4}\]
\[ \Rightarrow {PS}^2 = \frac{x^2 + 27 x^2}{36}\]
\[ \Rightarrow {PS}^2 = \frac{28 x^2}{36}\]
\[ \Rightarrow {PS}^2 = \frac{7 x^2}{9}\]
\[ \Rightarrow 9 {PS}^2 = 7 {PQ}^2\]
\[ \Rightarrow {PS}^2 = \left( \frac{x}{6} \right)^2 + \left( \frac{\sqrt{3}x}{2} \right)^2 \]
\[ \Rightarrow {PS}^2 = \frac{x^2}{36} + \frac{3 x^2}{4}\]
\[ \Rightarrow {PS}^2 = \frac{x^2 + 27 x^2}{36}\]
\[ \Rightarrow {PS}^2 = \frac{28 x^2}{36}\]
\[ \Rightarrow {PS}^2 = \frac{7 x^2}{9}\]
\[ \Rightarrow 9 {PS}^2 = 7 {PQ}^2\]
Hence, 9 PS2 = 7 PQ2.
Explanation:-
Given: QS = (1/3) QR = (x/3)
Therefore, ST = QT – QS = (x/2) – (x/3) = (x/6)
According to Pythagoras theorem, In ∆PQT, PQ^2 = QT^2 + PT^2 => x^2 = (x^2/4) + PT^2 => PT^2 = x^2 – (x^2/4) => PT^2 = (3x^2/4) => PT = (sqrt(3)x/2)
In ∆PST, PS^2 = ST^2 + PT^2 => PS^2 = (x^2/36) + (3x^2/4) => PS^2 = (x^2 + 27x^2)/36 => PS^2 = (28x^2/36) => PS^2 = (7x^2/9) => 9PS^2 = 7PQ^2
Hence, 9PS^2 = 7PQ^2.
Chapter 2 – Pythagoras Theorem- Text Book Solution
Problem Set 2 | Q 16 | Page 46
