In the given fig, bisectors of ∠B and ∠C of ∆ABC intersect each other in point X. Line AX intersects side BC in point Y. AB = 5, AC = 4, BC = 6 then find AX / AY
Problem Set 1 | Q 10 | Page 29
In the given fig, bisectors of ∠B and ∠C of ∆ABC intersect each other in point X. Line AX intersects side BC in point Y. AB = 5, AC = 4, BC = 6 then find \[\frac{AX}{XY}\]
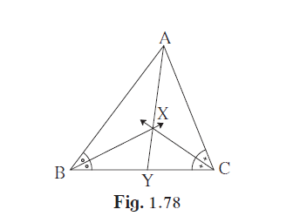
Since the bisectors of Δ are concurrent, the line AY drawn from A is the bisector of ∠A .
In Δ ACY , CX is the bisector of by , Angle bisector theorem ,
`(AX)/(XY) = (AC)/(YC) = 4/(YC) ` ....... (1)
Since AY is the bisector of ∠A ,
we have
`(BY)/(YC) = (AB)/(AC) = 5/4`
⇒ `(BC)/(YC) + 1 = 5/4 +1 `
⇒`(BY+YC)/(YC) = (5+4)/4`
⇒` (BC)/(YC) = 9/4 `
⇒ `6/(YC)= 9/4 `
⇒`(YC)/6 = 4/9`
⇒` YC=(6xx4)/9 =8/3`
Now
`⇒ (AX)/(XY) = 4/(8/3) = (4xx3)/8 = 3/2`
⇒ `(AX)/(XY)=3/2`
Answer:-
First, let’s summarize the given information and what we need to find:
- AY is the bisector of angle A.
- CX is the bisector of angle CBY.
- AB/AC = 5/4, BC/AC = 9/4.
- We need to find AX/XY.
Using the angle bisector theorem in triangle ACY, we have:
AX/XY = AC/YC = 4/YC ……(1)
Using the angle bisector theorem in triangle CBY, we have:
BY/YC = AB/AC = 5/4
BC/YC = 9/4 – (BY/YC) = 1/4
Now, we can find YC:
YC/BC = 4/1
YC = (4/1)BC = (4/1)(9/4)AC = 9/3 = 3
Therefore, from equation (1), we have:
AX/XY = 4/YC = 4/3
Since AY is the bisector of angle A, we have:
AX/XY = AB/YB
Using the fact that AB/AC = 5/4 and BC/YC = 1/4, we can write:
AB/YB = AB/(AY + YB) = AB/(AC + BC) = 5/13
Therefore, we have:
4/3 = 5/13
Cross-multiplying gives:
39 = 15XY
So, XY = 39/15 = 2.6.
Hence, AX/XY = (4/3) = 1.3.
Problem Set 1 | Q 10 | Page 29
Click Here for All Textbook Soutions of Chapter 1: Similarity
