In the following figure, AP ⊥ BC, AD || BC, then Find A(∆ABC): A(∆BCD).
Practice Set 1.1 | Q 4 | Page 6
In the following figure, AP ⊥ BC, AD || BC, then Find A(∆ABC): A(∆BCD).
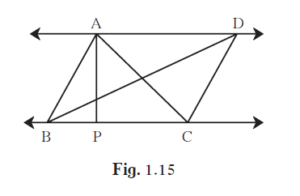
Given, AP ⊥ BC, and AD || BC. ΔABC and ΔBCD has the same base BC.
Areas of triangles with equal bases are proportional to their corresponding heights.
Since AP is the perpendicular distance between parallel lines AD and BC, the height of ΔABC and the height of ΔBCD are the same.
∴ `(A(ΔABC))/(A(ΔBCD)) = "AP"/"AP" = 1`
Hence A(ΔABC): A(ΔBCD) = 1: 1
Solution:-
The statement says that there are two triangles, ΔABC and ΔBCD, with the same base BC. It is also given that AP is perpendicular to BC, and AD is parallel to BC.
The statement then goes on to say that when two triangles have the same base, their areas are proportional to their corresponding heights. Because AP is the perpendicular distance between parallel lines AD and BC, the heights of ΔABC and ΔBCD are the same.
Therefore, the ratio of the areas of ΔABC and ΔBCD is equal to 1, since the heights are the same. Hence, the ratio of the areas of ΔABC and ΔBCD is 1:1.
Chapter 1. Similarity- Practice Set 1.1 – Page 5
Click Here for All Textbook Soutions of Chapter 1: Similarity
