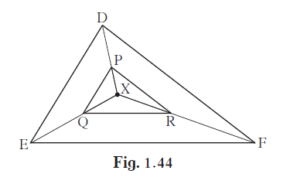
In the given figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.
Practice Set 1.2 | Q 10 | Page 15
In the given figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.
Proof : In Δ XDE, PQ || DE …….. ___________
`therefore “XP”/([ ]) = ([ ])/”QE”` ….. (I) (Basic proportionality theorem)
In Δ XEE, QR || EF …….. _________
`therefore ([ ])/([ ]) = ([ ])/([ ])` …….(II) _________________
`therefore ([ ])/([ ]) = ([ ])/([ ])` ……. from (I) and (II)
∴ seg PR || seg DE ……….. (converse of basic proportionality theorem)
Given:
Seg PQ || seg DE
seg QR || seg EF
In △DXE, PQ || DE
\[\frac{\text{XP}}{\text{PD}} = \frac{\text{XQ}}{\text{QE}} . . . \left( I \right) \left( \text{ By basic proportionality theorem } \right)\]
\[\]
In △XEF, QR || EF ....Given
\[\therefore \frac{\text{XQ}}{\text{QE}} = \frac{\text{XR}}{\text{RF}} . . . . . \left( II \right) \left( \text{ By basic proportionality theorem } \right)\]
\[\]
\[\therefore \frac{\text{XP}}{\text{PD}} = \frac{\text{XR}}{\text{RF}} \text{ From } \left( I \right)\text{ and } \left( II \right)\]
∴ seg PR || seg DF (Converse of basic proportional theorem)
Answer:_-
Given:
- Seg PQ || seg DE
- Seg QR || seg EF
To prove: seg PR || seg DF
Proof: In △DXE, PQ || DE ….(1) [Given]
Applying basic proportionality theorem in △DXE, we get: XP/PD = XQ/QE ….(2)
In △XEF, QR || EF ….(3) [Given]
Applying basic proportionality theorem in △XEF, we get: XQ/QE = XR/RF ….(4)
From equations (2) and (4), we get: XP/PD = XR/RF ….(5)
Applying converse of basic proportionality theorem in △PRF and using equation (5), we get: seg PR || seg DF ….(6)
Hence, we have proved that seg PR || seg DF.
Chapter 1. Similarity- Practice Set 1.2 – Page 15
Click Here for All Textbook Soutions of Chapter 1: Similarity
