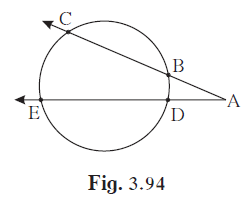
In the given figure, (1) m(arc CE) = 54°, m(arc BD) = 23°, find measure of ∠CAE.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 16 | Page 88
In the given figure,
(1) m(arc CE) = 54°, m(arc BD) = 23°, find measure of ∠CAE.
(2) If AB = 4.2, BC = 5.4, AE = 12.0, find AD.
(3) If AB = 3.6, AC = 9.0, AD = 5.4, find AE.
XW and YZ are two chords of a circle intersecting each other in the interior of the circle at T.
(1)
If two chords of a circle intersect each other in the interior of a circle then the measure of the angle between them is half the sum of measures of arcs intercepted by the angle and its opposite angle.
∴ ∠ZTX = `1/2`[m(arc ZX) + m(arc WY)] =`1/2 xx(68° + 44°) = 1/2 xx 112° = 56°`
Thus, the measure of ∠ZTX is 56º.
(2)
WT × TX = YT × TZ (Theorem of internal division of chords)
⇒ 4.8 × 8 = 6.4 × TZ
⇒ TZ =`(4.8xx8)/6.4 = 6`
(3)
WT × TX = YT × TZ (Theorem of internal division of chords)
⇒ WT × (WX − WT) = YT × (YZ − YT)
⇒ WT × (25 − WT) = 8 × (26 − 8)
⇒ 25WT − WT2 = 8 × 18 = 144
⇒ WT2 − 25WT + 144 = 0
⇒ WT2 − 16WT − 9WT + 144 = 0
⇒ WT(WT − 16) − 9(WT − 16) = 0
⇒ (WT − 16)(WT − 9) = 0
⇒ WT − 16 = 0 or WT − 9 = 0
⇒ WT = 16 or WT = 9
Explanation:-
XW and YZ are two chords of a circle intersecting each other in the interior of the circle at T. We are asked to find the measure of angle ZTX and the length of WT.
(1) According to a theorem, if two chords of a circle intersect each other in the interior of a circle, then the measure of the angle between them is half the sum of the measures of the arcs intercepted by the angle and its opposite angle. Therefore, we can calculate the measure of angle ZTX as follows: ∠ZTX = 1/2(m(arc ZX) + m(arc WY)) = 1/2(68° + 44°) = 56°.
(2) According to the theorem of internal division of chords, we know that WT * TX = YT * TZ. We are given that WT = 4.8, and we have calculated TZ as 6.4. Solving for TX, we get: WT * TX = YT * TZ 4.8 * TX = YT * 6.4 TX = (YT * 6.4)/4.8 TX = (YT * 4)/3 We don’t have enough information to calculate the length of YT, so we can’t determine the value of TX.
(3) Using the same theorem of internal division of chords, we know that WT * (WX – WT) = YT * (YZ – YT). We are given that WT = 4.8, WX = 25, YZ = 26, and we have calculated TZ as 6.4. Solving for WT, we get: WT * (WX – WT) = YT * (YZ – YT) 4.8 * (25 – 4.8) = YT * (26 – YT) 114.24 = YT^2 – 26YT YT^2 – 26YT – 114.24 = 0 Using the quadratic formula, we get: YT = (26 ± sqrt(26^2 + 4114.24))/2 YT = (26 ± sqrt(976.96))/2 YT = (26 ± 31.24)/2 YT = 28.12 or YT = -2.12 Since YT represents the length of a chord, it must be positive. Therefore, we have YT = 28.12. Using the equation WT * (WX – WT) = YT * (YZ – YT), we can solve for WT: WT * (WX – WT) = YT * (YZ – YT) WT * (25 – WT) = 28.12 * (26 – 28.12) WT^2 – 25WT + 144 = 0 Using the quadratic formula, we get: WT = (25 ± sqrt(25^2 – 4144))/2 WT = (25 ± 11)/2 WT = 16 or WT = 9 Therefore, the length of WT is either 16 or 9.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 16 | Page 88
Click Here to see All the Textbook solution of Circle
