In the given figure, seg AB is a diameter of a circle with centre C.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 10 | Page 86
In the given figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
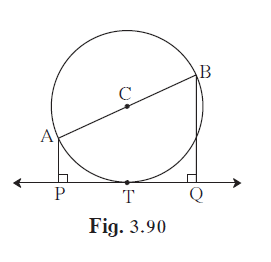
It is given that line PQ is a tangent, which touches the circle at point T.
∴ ∠CTP = ∠CTQ = 90º (Tangent at any point of a circle is perpendicular to the radius through the point of contact)
⇒ seg CT ⊥ line PQ
Also, seg AP ⊥ line PQ and seg BQ ⊥ line PQ.
∴ seg AP || seg CT || seg BQ
We know, the ratio of the intercepts made on a tranversal by three parallel lines is equal to the ratio of the corresponding intercepts made on any other transversal by the same parallel lines.
\[\therefore \frac{PT}{TQ} = \frac{AC}{CB}\]
\[ \Rightarrow \frac{PT}{TQ} = 1 \left( AC = CB \right)\]
\[ \Rightarrow PT = TQ\]
In ∆CPT and ∆CQT,
seg PT ≅ seg TQ (Proved)
∠CTP = ∠CTQ (90º each)
seg CT ≅ seg CT (Common)
∴ ∆CPT ≅ ∆CQT (RHS congruence criterion)
⇒ seg CP ≅ seg CQ (Corresponding parts of congruent triangles)
Hence proved.
Explanation:-
The problem states that line PQ is a tangent to the circle at point T. By the tangent theorem, we know that the tangent at any point of a circle is perpendicular to the radius through the point of contact. Thus, we have that angle CTP = angle CTQ = 90 degrees, and segment CT is perpendicular to line PQ.
Furthermore, we are given that segment AP is perpendicular to line PQ and that segment BQ is perpendicular to line PQ. Thus, we have that segments AP, CT, and BQ are all parallel. Therefore, we can use the property that the ratio of the intercepts made on a transversal by three parallel lines is equal to the ratio of the corresponding intercepts made on any other transversal by the same parallel lines.
Therefore, we have that PT/TQ = AC/CB. Since AC = CB, we have that PT/TQ = 1, which implies that PT = TQ.
Now, consider triangles CPT and CQT. We have that segment PT is congruent to segment TQ (proved above), angle CTP is congruent to angle CTQ (both are 90 degrees), and segment CT is congruent to itself. Thus, we have that triangles CPT and CQT are congruent by the RHS congruence criterion.
Therefore, we have that segment CP is congruent to segment CQ, since they are corresponding parts of congruent triangles. This implies that AC = BC, since CP and CQ are radii of the circle. Thus, we have proved that AC = BC, as desired.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 10 | Page 86
Click Here to see All the Textbook solution of Circle
