In the given figure, circles with centres X and Y touch internally at point Z
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 8 | Page 86
In the given figure, circles with centres X and Y touch internally at point Z . Seg BZ is a chord of bigger circle and it itersects smaller circle at point A. Prove that, seg AX || seg BY.
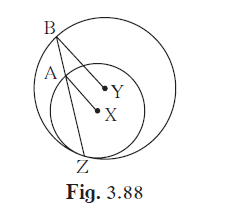
In the given figure, circles with centres X and Y touch internally at point Z . Seg BZ is a chord of bigger circle and it itersects smaller circle at point A. Prove that, seg AX || seg BY.
By theorem of touching circles, points Y, X, Z are collinear.
Now, seg XA ≅ seg XZ (Radii of circle with centre X)
∴∠XAZ = ∠XZA (Isosceles triangle theorem) .....(1)
Similarly, seg YB ≅ seg YZ (Radii of circle with centre Y)
∴∠BZY = ∠ZBY (Isosceles triangle theorem) .....(2)
From (1) and (2), we have
∠XAZ = ∠ZBY
If a pair of corresponding angles formed by a transversal on two lines is congruent, then the two lines are parallel.
∴ seg AX || seg BY (Corresponding angle test)
Explanation:-
The problem states that there are two circles, one with center X and the other with center Y, which touch internally at point Z. It is given that seg BZ is a chord of the bigger circle and intersects the smaller circle at point A. The task is to prove that seg AX || seg BY.
Using the theorem of touching circles, we know that points Y, X, and Z are collinear. This implies that the line passing through X and Y passes through Z as well.
Now, let us consider the triangles XAZ and ZBY. By definition, the radii of a circle are equal. Therefore, seg XA ≅ seg XZ, and seg YB ≅ seg YZ. This implies that XAZ and ZBY are isosceles triangles.
From the isosceles triangle theorem, we know that the base angles of an isosceles triangle are congruent. Thus, we can say that ∠XAZ = ∠XZA and ∠BZY = ∠ZBY.
Since ∠XAZ = ∠XZA and ∠BZY = ∠ZBY, we have ∠XAZ = ∠ZBY.
Using the corresponding angle test, we can conclude that seg AX || seg BY, since the pair of corresponding angles formed by a transversal on two lines is congruent.
Therefore, we have proved that seg AX || seg BY.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 8 | Page 86
Click Here to see All the Textbook solution of Circle
