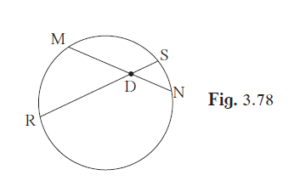
In the given figure, chord MN and chord RS intersect at point D. (1) If RD = 15, DS = 4, MD = 8 find DN (2) If RS = 18, MD = 9, DN = 8 find DS
Chapter 3 – Circle – Text Book Solution
Practice Set 3.5 | Q 2 | Page 82
In the given figure, chord MN and chord RS intersect at point D.
(1) If RD = 15, DS = 4, MD = 8 find DN
(2) If RS = 18, MD = 9, DN = 8 find DS
If two chords of a circle intersect each other in the interior of the circle, then the product of the lengths of the two segments of one chord is equal to the product of the lengths of the two segments of the other chord.
(1) MD × DN = RD × DS
⇒ 8 × DN = 15 × 4
⇒ DN = \[\frac{60}{8}\] = 7.5 units
(2) MD × DN = RD × DS
⇒ MD × DN = (RS − DS) × DS
⇒ 9 × 8 = (18 − DS) × DS
⇒ DS2 − 18DS + 72 = 0
⇒ DS2 − 12DS − 6DS + 72 = 0
⇒ DS(DS − 12) − 6(DS − 12) = 0
⇒ (DS − 12)(DS − 6) = 0
⇒ DS − 12 = 0 or DS − 6 = 0
⇒ DS = 12 units or DS = 6 units
Explanation:-
The given problem is about the properties of chords in a circle. If two chords of a circle intersect each other in the interior of the circle, then the product of the lengths of the two segments of one chord is equal to the product of the lengths of the two segments of the other chord.
Using this property, we can find the length of DN in terms of MD and RD & DS. From the first equation MD × DN = RD × DS, we get 8 × DN = 15 × 4, which gives DN = 7.5 units.
Now, we use this result to find the value of DS in terms of MD and RD. From the second equation, we have MD × DN = RD × DS. Substituting the value of DN as 7.5 units, we get MD × 7.5 = (RS – DS) × DS. We know that RS = 18 units and MD = 9 units, so we get 9 × 7.5 = (18 – DS) × DS.
Simplifying, we get DS^2 – 18DS + 72 = 0. Solving this quadratic equation, we get DS = 12 units or DS = 6 units.
Therefore, the possible values of DS are 12 units or 6 units, depending on the lengths of MD and RD.
Chapter 3 – Circle – Text Book Solution
Practice set 3.5 | Q 2 | Page 82
Click Here to see All the Textbook solution of Circle
