Spread the love

In figure 3.61, chords AC and DE intersect at B. If ∠ ABE = 108°, m(arc AE) = 95°, find m(arc DC).

Chapter 3 – Circle – Text Book Solution

Practice Set 3.4 | Q 78| Page 74

In figure 3.61, chords AC and DE
intersect at B.

If ∠ ABE = 108°, m(arc AE) = 95°, find m(arc DC).

solution

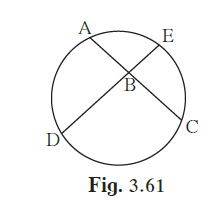
We know, if two chords of a circle intersect each other in the interior of a circle, then the measure of the angle between them is half the sum of measures of the arcs intercepted by the angle and its opposite angle.
∴ ∠ABE = \[\frac{1}{2}\] [m(arc AE) + m(arc DC)]
⇒ m(arc AE) + m(arc DC) = 2∠ABE
⇒ 95º + m(arc DC) = 2 × 108º
⇒ m(arc DC) = 216º − 95º = 121º
Thus, the measure of arc DC is 121º.

Explanation:-

To find: The measure of arc DC

Given: Chords AB and DE of a circle intersect at point B inside the circle, and angle ABE measures 108 degrees.

Solution:

Let arc AE be x degrees, then arc DC will be (360-x) degrees because they are opposite angles of the circle.

So, applying the formula we get:

∠ABE = [\frac{1}{2}] [m(arc AE) + m(arc DC)]

⇒ m(arc AE) + m(arc DC) = 2∠ABE

⇒ x + (360-x) = 2 × 108º

⇒ 360 = 216º + x

⇒ x = 360º − 216º = 144º

Thus, the measure of arc AE is 144 degrees.

Now, to find the measure of arc DC:

m(arc DC) = 360º – m(arc AE)

m(arc DC) = 360º – 144º = 216º

Therefore, the measure of arc DC is 216 degrees.

Chapter 3 – Circle – Text Book Solution

Practice set 3.4 | Q 8 | Page 74

Click Here to see All the Textbook solution of Circle