In the given figure, m(arc NS) = 125°, m(arc EF) = 37°, find the measure ∠ NMS.
Chapter 3 – Circle – Text Book Solution
Practice Set 3.4 | Q 7 | Page 74
In the given figure, m(arc NS) = 125°, m(arc EF) = 37°, find the measure ∠ NMS.
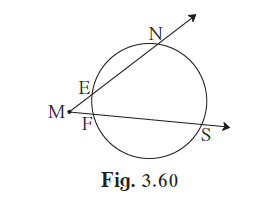
We know, if two lines containing chords of a circle intersect each other outside the circle, then the measure of the angle between them is half the difference in measures of the arcs intercepted by the angle.
∴ ∠NMS = \[\frac{1}{2}\] [m(arc NS) − m(arc EF)]
⇒ ∠NMS = \[\frac{1}{2} \times \left( 125^\circ - 37^\circ \right) = \frac{1}{2} \times 88^\circ\]= 44º
Thus, the measure of ∠NMS is 44º.
Explanation:-
We are given that two lines containing chords of a circle intersect each other outside the circle. We need to find the measure of the angle between them.
We know that if two lines containing chords of a circle intersect each other outside the circle, then the measure of the angle between them is half the difference in measures of the arcs intercepted by the angle.
Let us denote the intersection point of the two lines by S. Let EF and NS be the chords of the circle intersecting at S. We are given that m(arc NS) = 125° and m(arc EF) = 37°.
Therefore, the measure of the angle between the two lines containing chords NS and EF is given by:
∠NMS = 1/2 [m(arc NS) – m(arc EF)]
Substituting the given values, we get:
∠NMS = 1/2 (125° – 37°)
∠NMS = 1/2 x 88°
∠NMS = 44°
Hence, we have found that the measure of the angle between the two lines containing chords NS and EF is 44°.
Chapter 3 – Circle – Text Book Solution
Practice set 3.4 | Q 7 | Page 74
Click Here to see All the Textbook solution of Circle
