In adjoining figure, seg PS ⊥ seg RQ, seg QT ⊥ seg PR. If RQ = 6, PS = 6 and PR = 12, then Find QT.
Practice Set 1.1 | Q 3 | Page 6
In adjoining figure, seg PS ⊥ seg RQ, seg QT ⊥ seg PR. If RQ = 6, PS = 6 and PR = 12, then Find QT.
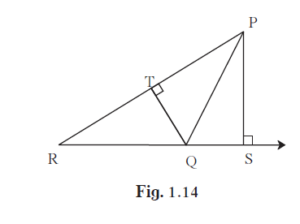
`{:("seg PS ⊥ seg RQ"), ("seg QT ⊥ seg PR"), ("RQ = 6, PS = 6 and PR = 12"):} }"Given"`
With base PR and height QT,
A(Δ PQR) = `1/2` × PR × QT ...(1)
With base QR and height PS,
A(Δ PQR) = `1/2` × QR × PS ...(2)
The ratio of areas of two triangles is equal to the ratio of the product of their base and corresponding heights.
From (1) and (2),
`"A(Δ PQR)"/"A(Δ PQR)" = (1/2 × "PR × QT")/(1/2 × "QR ×PS")`
`1/1 = ("PR"×"QT")/("QR"×"PS")`
PR × QT = QR × PS
QT = `("QR × PS")/"PR"`
QT = `(6 × 6)/12`
QT = `3/1`
Hence, the measure of side QT is 3 units.
Solution2:- “seg PS ⊥ seg RQ, seg QT ⊥ seg PR, RQ = 6, PS = 6 and PR = 12. Given.
With base PR and height QT, Area of triangle PQR = 1/2 × PR × QT …(1)
With base QR and height PS, Area of triangle PQR = 1/2 × QR × PS …(2)
The ratio of the areas of two triangles is equal to the ratio of the product of their base and corresponding heights.
From equations (1) and (2), Area of triangle PQR / Area of triangle PQR = (1/2 × PR × QT) / (1/2 × QR × PS) 1/1 = (PR × QT) / (QR × PS) PR × QT = QR × PS
Substituting the given values, we get: QT = (QR × PS) / PR QT = (6 × 6) / 12 QT = 3
Hence, the measure of side QT is 3 units.”
Chapter 1. Similarity- Practice Set 1.1 – Page 5
Click Here for All Textbook Soutions of Chapter 1: Similarity
