In ∆PQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR
Problem Set 1 | Q 9 | Page 28
In ∆PQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR intersect side PQ and side PR in points X and Y respectively. Prove that XY || QR.
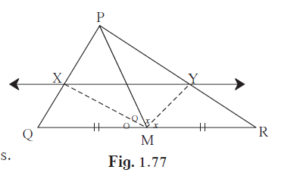
In △PMQ, ray MX is bisector of △PMQ.
\[\therefore \frac{PX}{XQ} = \frac{MQ}{MP}\] .......... (I) theorem of angle bisector.
In △PMR, ray MY is bisector of△PMR.
\[\therefore \frac{PY}{YR} = \frac{MR}{MP}\] .......... (II) theorem of angle bisector.
\[\frac{MP}{MQ} = \frac{MP}{MR}\] ......... M is the midpoint QR, hence MQ = MR.
\[\therefore \frac{PX}{XQ} = \frac{PY}{YR}\]
∴XY || QR .......... converse of basic proportionality theorem.
Answer:-
In the given problem, we are given a triangle PMQ in which ray MX is the bisector of angle PMQ and ray MY is the bisector of angle PMR. We need to prove that XY is parallel to QR.
Using the angle bisector theorem, we know that in a triangle, the angle bisector divides the opposite side into two segments that are proportional to the other two sides.
Thus, using the angle bisector theorem in triangle PMQ, we get:
PX/XQ = MQ/MP …………… (I)
Similarly, using the angle bisector theorem in triangle PMR, we get:
PY/YR = MR/MP …………… (II)
Now, we need to prove that XY is parallel to QR.
To do this, we will use the converse of the basic proportionality theorem. According to the converse of the basic proportionality theorem, if a line is drawn parallel to one side of a triangle and intersects the other two sides, then it divides those two sides in the same ratio.
So, let’s assume that XY is parallel to QR. Then, according to the converse of the basic proportionality theorem, we have:
PX/XQ = PY/YR
Substituting the values of PX/XQ and PY/YR from equations (I) and (II), we get:
MQ/MP = MR/MP
Since M is the midpoint of QR, we have:
MQ = MR
Thus, the above equation becomes:
MP/MP = 1
Therefore, our assumption that XY is parallel to QR is true, and we have proved that XY is parallel to QR using the converse of the basic proportionality theorem.
Problem Set 1 | Q 9 | Page 28
Click Here for All Textbook Soutions of Chapter 1: Similarity
