In ∆ABC, B - D - C and BD = 7, BC = 20 then Find following ratio. A(∆ ABD)/A(∆ ADC)
Problem Set 1 | Q 2.1 | Page 27
In ∆ABC, B – D – C and BD = 7, BC = 20 then Find following ratio.
A(∆ ABD)/A(∆ ADC)
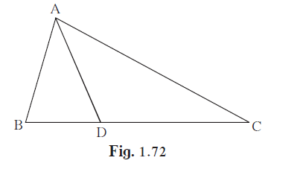
BC = BD + DC ...[B - D - C]
DC = BC - BD
DC = 20 - 7
DC = 13
Ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights.
∴ A(∆ ABD)/A(∆ ADC) = (1/2 × AX × BD)/(1/2 × AX × DC)
∴ A(∆ ABD)/A(∆ ADC) = BD/DC
∴ A(∆ ABD)/A(∆ ADC) = 7/13
Answer:_
Step 1: BC = BD + DC …[B – D – C]
This step involves adding the lengths of two line segments BD and DC to find the length of BC. The statement [B – D – C] is a shorthand way of indicating that points B, D, and C are collinear, or lie on the same line segment.
Step 2: DC = BC – BD
This step involves subtracting the length of BD from BC to find the length of DC. This is possible because we know that BC = BD + DC (from Step 1), so rearranging the equation gives DC = BC – BD.
Step 3: DC = 20 – 7
This step substitutes the values given in the problem for BC and BD, which are 20 and 7, respectively. This gives us the value of DC as 13.
Step 4: Ratio of areas of two triangles
This step involves applying the formula for the ratio of the areas of two triangles to find the ratio of the areas of ∆ABD and ∆ADC. The formula states that the ratio of the areas of two triangles is equal to the ratio of the products of their bases and corresponding heights.
Step 5: A(∆ABD)/A(∆ADC) = (1/2 * AX * BD)/(1/2 * AX * DC)
This step applies the formula from Step 4 to the triangles ∆ABD and ∆ADC. We know that the base of both triangles is AX, and their corresponding heights are BD and DC, respectively.
Step 6: A(∆ABD)/A(∆ADC) = BD/DC
This step simplifies the expression obtained in Step 5 by cancelling the common factor of (1/2 * AX) from both the numerator and denominator. This gives us the ratio of BD to DC.
Step 7: A(∆ABD)/A(∆ADC) = 7/13
This step substitutes the given values for BD and DC into the expression obtained in Step 6, which gives us the ratio of the areas of the triangles ∆ABD and ∆ADC as 7/13.
Problem Set 1 | Q 2.1 | Page 27
Click Here for All Textbook Soutions of Chapter 1: Similarity
