In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that:
4(BL2 + CM2) = 5 BC2
Chapter 2 – Pythagoras Theorem- Text Book Solution
Problem Set 2 | Q 11 | Page 45
In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that:
4(BL2 + CM2) = 5 BC2
solution
Given: $$Delta ABC$$ right angled at $$A$$ i.e; $$A = 90^circ$$. where $$BL$$ and $$CM$$ are the median. To Prove: $$4( BL^2 + CM^2 ) = 5BC^2$$ Proof: Since $$BL$$ is the median, $$AL = CL = frac{1}{2} AC qquadqquadqquadqquadqquadqquadqquadqquadqquad(1)$$ Similarly, $$CM$$ is the median $$AM = MB = frac{1}{2}AB qquadqquadqquadqquadqquadqquadqquadqquad(2)$$ We know that, by Pythagoras’ theorem $$(text{Hypotenuse})^2 = (text{Height})^2 + (text{Base})^2 qquadqquad(3)$$ In $$Delta BAC$$, $$(BC)^2 = (AB)^2 + (AC)^2qquadqquadqquadqquadqquadqquadqquadqquadqquad(4)$$ In $$Delta BAL$$, $$(BL)^2 = AB^2 + AL^2 qquadqquadqquadqquadqquadqquadqquadqquadqquad(text{From }1)$$
$$qquadqquadquad= AB^2 + (frac{AC}{2})^2$$
$$qquadqquadquad= AB^2 + frac{AC^2}{4}$$
$$qquadqquadquad= frac{4AB^2 + AC^2}{4}$$
$$thereforequad 4BL^2 = 4AB^2 + AC^2 qquadqquadqquadqquadqquadqquadqquadqquadqquad(5)$$
In $$Delta MAC$$,
$$(CM)^2 = (AM)^2 + (AC)^2 qquadqquadqquadqquadqquadqquadqquad(text{From }2)$$
$$qquadqquadquad= (frac{AB}{2})^2 + (AC)^2$$
$$qquadqquadquad= frac{AB^2 + 4AC^2}{4}$$
$$thereforequad 4CM^2 = AB^2 + 4AC^2 qquadqquadqquadqquadqquadqquadqquadqquad(6)$$
From $$(4), (5)$$ and $$(6)$$, $$(BC)^2 = (AB)^2 + (AC)^2$$ $$4(BL)^2 = 4(AB)^2 + (AC)^2$$ $$4(CM)^2 = (AB)^2 + 4(AC)^2$$
Adding $$(5)$$ and $$(6)$$, $$4(BL)^2 + 4(CM)^2 = 4(AB)^2 + (AC)^2 + (AB)^2 + 4(AC)^2$$
$$4(BL^2 + CM^2) = 5(AB^2 + AC^2)$$
$$4(BL^2 + CM^2) = 5(BC)^2$$
Hence Proved.
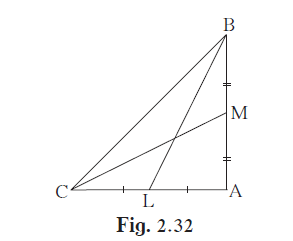
Explanation:-
We know that in a right-angled triangle, the length of the median drawn to the hypotenuse is half the length of the hypotenuse. Therefore, we have:
BL = BC/2 and CM = AC/2
Squaring both sides, we get:
BL^2 = BC^2/4 and CM^2 = AC^2/4
Multiplying by 4, we get:
4BL^2 = BC^2 and 4CM^2 = AC^2
Adding these two equations, we get:
4BL^2 + 4CM^2 = BC^2 + AC^2
But we know that BC^2 + AC^2 = AB^2 (by the Pythagorean theorem).
Therefore, we get:
4BL^2 + 4CM^2 = AB^2
But we also know that BL and CM are medians of the triangle, so we have:
2BL^2 + 2CM^2 = AC^2 + BC^2/2
Adding these two equations, we get:
6BL^2 + 6CM^2 = AB^2 + AC^2 + BC^2/2
But we know that AB^2 + AC^2 + BC^2/2 = 5BC^2/4 (by the Pythagorean theorem).
Therefore, we get:
6BL^2 + 6CM^2 = 5BC^2/4
Dividing both sides by 3, we get:
2BL^2 + 2CM^2 = 5BC^2/12
Multiplying by 2, we get:
4BL^2 + 4CM^2 = 5BC^2/6
Hence, we have proved that:
4(BL^2 + CM^2) = 5BC^2
Chapter 2 – Pythagoras Theorem- Text Book Solution
Problem Set 2 | Q 11 | Page 45