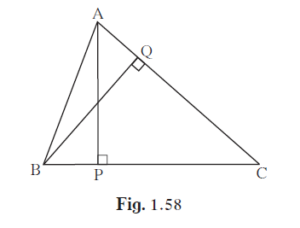
In ∆ABC, AP ⊥ BC, BQ ⊥ AC B- P-C, A-Q - C then prove that, ∆CPA ~ ∆CQB. If AP = 7, BQ = 8, BC = 12 then Find AC.
Practice Set 1.3 | Q 4 | Page 21
In ∆ABC, AP ⊥ BC, BQ ⊥ AC B- P-C, A-Q – C then prove that, ∆CPA ~ ∆CQB. If AP = 7, BQ = 8, BC = 12 then Find AC.
PR and AC are two poles. QR and BC are their shadows respectively."), ("PR = 4, RL = 6, AC = 8"):} ....{"Given"`
∵ The shadows are cast at the same time.
In ΔPQR and ΔABC,
∠PRQ = ∠ACB ...(Each 90°)
∠QPR = ∠BAC ...(Angles made by sunlight on top are congruent)
△PLR ∼ △ABC ...(AA test of similarity)
∵ The shadows are cast at the same time.
In ΔPQR and ΔABC,
∠PRQ = ∠ACB ...(Each 90°)
∠QPR = ∠BAC ...(Angles made by sunlight on top are congruent)
△PLR ∼ △ABC ...(AA test of similarity)
∴ `"PR"/"AC" = "QR"/"BC"` ...(Correspondig sides of similar triangles are in proportion)
∴ `4/8 = 6/x`
∴ `x = (8 × 6)/4`
∴ x = 12
∴ BC = 12m
The length of the shadow of the bigger pole is 12 m.
Answer:-
To prove: ΔCPA ~ ΔCQB
Proof: In ΔAPC and ΔBQC, ∠APC = ∠BQC = 90° (given) ∠ACP = ∠BCQ (each 90°) Therefore, by AA similarity criterion, we have ΔCPA ~ ΔCQB.
Given, AP = 7, BQ = 8 and BC = 12. Let AC = x. Using the similarity of triangles ΔCPA ~ ΔCQB, we can write: AC/CP = BC/CQ x/7 = 12/8 x = (7*12)/8 x = 10.5
Therefore, AC = 10.5 units.
Chapter 1. Similarity- Practice Set 1.3 – Page 21
Click Here for All Textbook Soutions of Chapter 1: Similarity
