From the top of a lighthouse, an observer looking at a ship makes angle o
Chapter 6 – Trigonometry – Text Book Solution
Practice Set 6.2| Q 2| Page 137
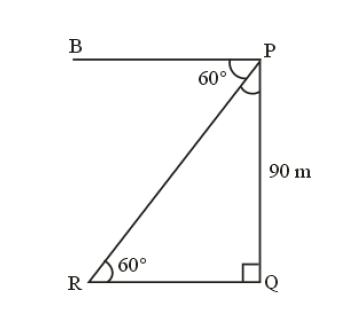
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse. (√3 =1.73)
Solution
Let’s denote the distance from the ship to the base of the lighthouse as “d”. We can draw a right-angled triangle, where the top of the lighthouse is at the right angle, the observer is at the top of the lighthouse, and the line of sight from the observer to the ship is the opposite side of the triangle. The height of the lighthouse is the adjacent side of the triangle.
From the triangle, we can see that:
tan(60°) = 90/d
tan(60°) is equal to √3, so we can simplify the equation to:
√3 = 90/d
Multiplying both sides by d, we get:
d√3 = 90
Dividing both sides by √3, we get:
d = 90/√3
Rationalizing the denominator by multiplying both sides by √3/√3, we get:
d = 90√3/3
Simplifying the right-hand side, we get:
d = 30√3
d = 30 x 1.73 = 51.90 m
Therefore, the ship is located approximately 51.90 m meters away from the lighthouse.
Chapter 6 – Trigonometry – Text Book Solution
Practice set 6.2 |Q 2| P 137
Click Here to see All the Textbook solution of Geometric Construction
