In the given figure, seg AD ⊥ side BC, seg BE ⊥ side AC, seg CF ⊥ side AB.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 25 | Page 90
In the given figure, seg AD ⊥ side BC, seg BE ⊥ side AC, seg CF ⊥ side AB. Ponit O is the orthocentre. Prove that , point O is the incentre of ∆DEF.
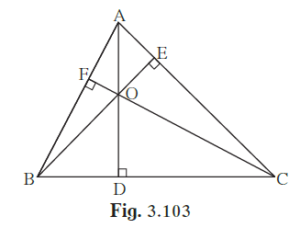
It is given that seg AD ⊥ side BC, seg BE ⊥ side AC and seg CF ⊥ side BC. O is the orthocentre of ∆ABC.
Join DE, EF and DF.
∠AFO + ∠AEO = 90º + 90º = 180º
∴ Quadrilateral AEOF is cyclic. (If a pair of opposite angles of a quadrilateral is supplementary, the quadrilateral is cyclic)
⇒ ∠OAE = ∠OFE .....(1) (Angles inscribed in the same arc are congruent)
∠BFO + ∠BDO = 90º + 90º = 180º
∴ Quadrilateral BFOD is cyclic. (If a pair of opposite angles of a quadrilateral is supplementary, the quadrilateral is cyclic)
⇒ ∠OBD = ∠OFD .....(2) (Angles inscribed in the same arc are congruent)
In ∆ACD,
∠DAC + ∠ACD = 90º .....(3) (Using angle sum property of triangle)
In ∆BCE,
∠BCE + ∠CBE = 90º .....(4) (Using angle sum property of triangle)
From (3) and (4), we get
∠DAC + ∠ACD = ∠BCE + ∠CBE
⇒ ∠DAC = ∠CBE .....(5)
From (1), (2) and (5), we get
∠OFE = ∠OFD
⇒ OF is the bisector of ∠EFD.
Similarly, OE and OD are the bisectors of ∠DEF and ∠EDF, respectively.
Hence, O is the incentre of ∆DEF. (Incentre of a triangle is the point of intersection of its angle bisectors)
Explanation:-
Given: In triangle ABC, seg AD ⊥ BC, seg BE ⊥ AC and seg CF ⊥ BC. O is the orthocentre of ∆ABC. DE, EF, and DF are joined.
To prove: O is the incentre of ∆DEF.
Proof:
- We know that AF ⊥ OE and AE ⊥ OF. Therefore, ∠AFO + ∠AEO = 90° + 90° = 180°. Hence, quadrilateral AEOF is cyclic. (If a pair of opposite angles of a quadrilateral is supplementary, the quadrilateral is cyclic).
- Using the property that angles inscribed in the same arc are congruent, we get ∠OAE = ∠OFE (from step 1).
- We also know that BF ⊥ OD and BD ⊥ OF. Therefore, ∠BFO + ∠BDO = 90° + 90° = 180°. Hence, quadrilateral BFOD is cyclic. (If a pair of opposite angles of a quadrilateral is supplementary, the quadrilateral is cyclic).
- Again using the property that angles inscribed in the same arc are congruent, we get ∠OBD = ∠OFD (from step 3).
- In ∆ACD, we know that ∠DAC + ∠ACD = 90° (using angle sum property of a triangle).
- In ∆BCE, we know that ∠BCE + ∠CBE = 90° (using angle sum property of a triangle).
- From step 5 and 6, we get ∠DAC + ∠ACD = ∠BCE + ∠CBE.
- Using step 1, 2, and 7, we get ∠OFE = ∠OFD and ∠OAE = ∠OBD.
- Therefore, OF is the bisector of ∠EFD, OE is the bisector of ∠DEF, and OD is the bisector of ∠EDF.
- Hence, O is the incentre of ∆DEF. (Incentre of a triangle is the point of intersection of its angle bisectors).
Therefore, O is the incentre of ∆DEF, which completes the proof.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 25 | Page 90
Click Here to see All the Textbook solution of Circle
