In the given figure, two circles intersect each other at points A and E. Their common sec
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 24 | Page 90
In the given figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that ▢ABCD is cyclic.
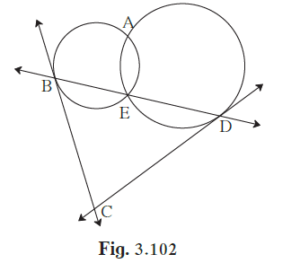
It is given that two circles intersect each other at points A and E.
Join AE, AB and AD.
The angle between a tangent of a circle and a chord drawn from the point of contact is congruent to the angle inscribed in the arc opposite to the arc intercepted by that angle.
BC is the tangent to the smaller circle and BE is the chord.
∴ ∠EBC = ∠BAE .....(1)
Also, CD is the tangent to the bigger circle and ED is the chord.
∴ ∠EDC = ∠DAE .....(2)
Adding (1) and (2), we get
∠EBC + ∠EDC = ∠BAE + ∠DAE
⇒ ∠EBC + ∠EDC = ∠BAD .....(3)
In ∆BCD,
∠DBC + ∠BDC + ∠BCD = 180º .....(4) (Angle sum property)
From (3) and (4), we get
∠BAD + ∠BCD = 180º
In quadrilateral ABCD,
∠BAD + ∠BCD = 180º
Therefore, quadrilateral ABCD is cyclic. (If a pair of opposite angles of a quadrilateral is supplementary, the quadrilateral is cyclic)
Explanation:-
We are given two circles that intersect each other at points A and E. To prove that quadrilateral ABCD is cyclic, we join AE, AB, and AD.
We know that the angle between a tangent of a circle and a chord drawn from the point of contact is congruent to the angle inscribed in the arc opposite to the arc intercepted by that angle.
BC is the tangent to the smaller circle and BE is the chord. Therefore, we have:
∠EBC = ∠BAE …..(1)
Similarly, CD is the tangent to the bigger circle and ED is the chord. Therefore, we have:
∠EDC = ∠DAE …..(2)
Adding equations (1) and (2), we get:
∠EBC + ∠EDC = ∠BAE + ∠DAE ⇒ ∠EBC + ∠EDC = ∠BAD …..(3)
In triangle BCD, we know that:
∠DBC + ∠BDC + ∠BCD = 180° …..(4) (Angle sum property of a triangle)
From equations (3) and (4), we get:
∠BAD + ∠BCD = 180°
In quadrilateral ABCD, the sum of opposite angles is supplementary if and only if the quadrilateral is cyclic. Therefore, quadrilateral ABCD is cyclic.
Hence, we have proved that quadrilateral ABCD is cyclic.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 24 | Page 90
Click Here to see All the Textbook solution of Circle
