In the given figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R, S and P, Q respectively. Prove that : seg SQ || seg RP.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 23 | Page 90
In the given figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R, S and P, Q respectively. Prove that : seg SQ || seg RP.
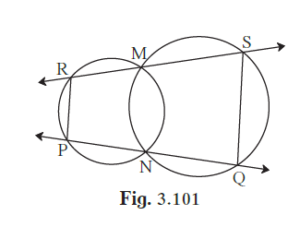
It is given that two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R, S and P, Q.
Join MN.
Quadrilateral PRMN is a cyclic quadrilateral.
∴ ∠PRM = ∠MNQ .....(1) (Exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle)
Quadrilateral QSMN is a cyclic quadrilateral.
∴ ∠QSM = ∠MNP .....(2) (Exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle)
Adding (1) and (2), we get
∠PRM + ∠QSM = ∠MNQ + ∠MNP .....(3)
Now,
∠MNQ + ∠MNP = 180º .....(4) (Angles in linear pair)
From (3) and (4), we get
∠PRM + ∠QSM = 180º
Now, line RS is transversal to the lines PR and QS such that
∠PRS + ∠QSR = 180º
∴ seg SQ || seg RP (If the interior angles formed by a transversal of two distinct lines are supplementary, then the two lines are parallel)
Hence proved.
Explanation:-
We are given two circles that intersect at points M and N. Secants drawn through M and N intersect the circles at points R, S and P, Q. We are required to prove that SQ is parallel to RP.
We know that quadrilateral PRMN is a cyclic quadrilateral. Therefore, the exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle. Hence, we have: ∠PRM = ∠MNQ ……(1)
Similarly, quadrilateral QSMN is a cyclic quadrilateral. Therefore, the exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle. Hence, we have: ∠QSM = ∠MNP ……(2)
Adding equations (1) and (2), we get: ∠PRM + ∠QSM = ∠MNQ + ∠MNP ……(3)
Now, we know that ∠MNQ + ∠MNP = 180º as they are angles in a linear pair. Hence, we can substitute this in equation (3) to get: ∠PRM + ∠QSM = 180º ……(4)
We also know that line RS is transversal to the lines PR and QS such that ∠PRS + ∠QSR = 180º as they are supplementary angles. Therefore, we can conclude that seg SQ || seg RP as per the theorem stating that if the interior angles formed by a transversal of two distinct lines are supplementary, then the two lines are parallel.
Hence, we have proved that SQ is parallel to RP.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 23 | Page 89
Click Here to see All the Textbook solution of Circle
