In the given figure, circles with centres C and D touch internally at point E.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 19 | Page 88
In the given figure, circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the outer circle intersects inner circle at point A. Prove that, seg EA ≅ seg AB.
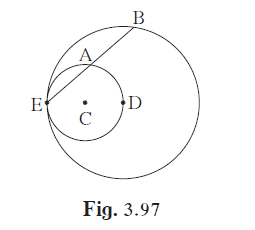
Circles with centres C and D touch internally at point E.
Join ED.
By theorem of touching circles, points E, C and D are collinear.
Since D lies on the inner circle with centre C, therefore, ED is the diameter of the inner circle.
∴ ∠EAD = 90º (Angle inscribed in a semi-circle is a right angle)
EB is the chord of the outer circle with centre D.
∴ Point A is the mid-point of chord EB. (Perpendicular drawn from the centre of a circle on its chord bisects the chord)
⇒ seg EA ≅ seg AB
Explanation:-
Two circles with centers C and D are given, and they touch internally at point E. The line ED is then drawn. According to the theorem of touching circles, since points E, C, and D all lie on the same line, they are collinear.
Since point D lies on the inner circle with center C, the diameter of the inner circle is ED. Thus, by the definition of a semicircle, angle EAD is a right angle, measuring 90 degrees.
Next, we know that EB is a chord of the outer circle with center D. By the definition of a perpendicular drawn from the center of a circle, any perpendicular line drawn from the center of a circle to its chord bisects the chord. Therefore, point A is the midpoint of chord EB. This leads to the conclusion that segment EA is congruent to segment AB.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 19 | Page 88
Click Here to see All the Textbook solution of Circle
