Spread the love

In the given figure, P is the point of contact. (1) If m(arc PR) = 140°, ∠ POR = 36°, find m(arc PQ)

Chapter 3 – Circle – Text Book Solution

Problem Set 3 | Q 18 | Page 88

In the given figure, P is the point of contact.
(1) If m(arc PR) = 140°, ∠ POR = 36°, find m(arc PQ)
(2) If OP = 7.2, OQ = 3.2, find OR and QR
(3) If OP = 7.2, OR = 16.2, find QR.

solution

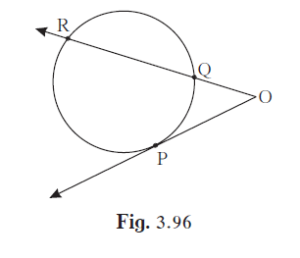
Join PQ.

(1)
The measure of an inscribed angle is half of the measure of the arc intercepted by it.
∴ ∠PQR =\[\frac{1}{2}\] m(arc PR) = \[\frac{1}{2} \times 140°\] = 70º

In ∆POQ,
∠PQR = ∠POQ + ∠OPQ (Measure of an exterior angle of a triangle is equal to the sum of its remote interior angles)
⇒ 70º = 36º + ∠OPQ
⇒ ∠OPQ = 70º − 36º = 34º
The angle between a tangent of a circle and a chord drawn from the point of contact is congruent to the angle inscribed in the arc opposite to the arc intercepted by that angle.
∴ ∠PRQ = ∠OPQ = 34º
Now,
∠PRQ = \[\frac{1}{2}\]m(arc PQ) (The measure of an inscribed angle is half of the measure of the arc intercepted by it)
⇒ m(arc PQ) = 2∠PRQ = 2 × 34º = 68º
(2)
OP is the tangent and OQR is the secant.
∴ OQ × OR = OP² (Tangent secant segment theorem)
⇒ 3.2 × OR = (7.2)²

⇒ OR = \[\frac{7 . 2 \times 7 . 2}{3 . 2}\] = 16.2

∴ QR = OR − OQ = 16.2 − 3.2 = 13

(3)
OP is the tangent and OQR is the secant.
∴ OQ × OR = OP² (Tangent secant segment theorem)
⇒ OQ × 16.2 = (7.2)²
⇒ OQ = \[\frac{7 . 2 \times 7 . 2}{16 . 2}\] = 3.2

∴ QR = OR − OQ = 16.2 − 3.2 = 13

Explanation:-

Here is a detailed explanation of the given answer:

First, the line segment PQ is drawn.
- This sets up the context for the subsequent angle and arc measurements.
The measure of the angle PQR is found using the inscribed angle theorem.
- The inscribed angle theorem states that the measure of an inscribed angle is half the measure of the arc intercepted by it.
- Therefore, ∠PQR = 1/2 m(arc PR) = 1/2 x 140° = 70°.
Using the fact that the measure of an exterior angle of a triangle is equal to the sum of its remote interior angles, the measure of angle OPQ is found.
- Specifically, ∠PQR = ∠POQ + ∠OPQ.
- Therefore, 70° = 36° + ∠OPQ, which yields ∠OPQ = 34°.
The angle between a tangent of a circle and a chord drawn from the point of contact is congruent to the angle inscribed in the arc opposite to the arc intercepted by that angle.
- In other words, ∠PRQ = ∠OPQ.
Using the inscribed angle theorem again, the measure of arc PQ is found.
- Specifically, ∠PRQ = 1/2 m(arc PQ).
- Therefore, m(arc PQ) = 2∠PRQ = 2 x 34° = 68°.
The tangent secant segment theorem is applied to find the length of OR.
- Specifically, OP^2 = OQ x OR.
- Plugging in the given values, this becomes 3.2 x OR = 7.2^2.
- Solving for OR yields OR = (7.2)^2 / 3.2 = 16.2.
Using the fact that QR = OR – OQ, the length of QR is found.
- Specifically, QR = OR – OQ = 16.2 – 3.2 = 13.
The tangent secant segment theorem is applied again to find the length of OQ.
- Specifically, OQ x OR = OP^2.
- Plugging in the given values, this becomes OQ x 16.2 = (7.2)^2.
- Solving for OQ yields OQ = (7.2)^2 / 16.2 = 3.2.
Using the fact that QR = OR – OQ again, the length of QR is confirmed to be 13.

Chapter 3 – Circle – Text Book Solution

Problem Set 3 | Q 18 | Page 88

Click Here to see All the Textbook solution of Circle