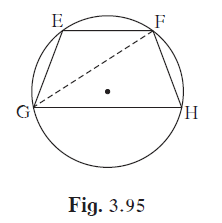
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 17 | Page 88
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof
solution
we have:
m(arc EG) = m(arc FH)
Hence, proved.
Proof: Draw seg GF.
∠EFG = ∠FGH .....property of alternate angles of parallel lines (I)
∠EFG = \[\frac{1}{2}m\left( arc EG \right)\] .....inscribed angle theorem (II)
∠FGH = \[\frac{1}{2}m\left( arc FH \right)\] .....inscribed angle theorem (III)
∴ m(arc EG) = \[m\left( arc FH \right)\] from (I), (II), (III)
Explanation:-
To prove: m(arc EG) = m(arc FH)
Proof:
Draw segment GF such that EF || GH.
By the property of alternate angles of parallel lines, we have:
∠EFG = ∠FGH ……(i)
By the inscribed angle theorem, we have:
∠EFG = 1/2m(arc EG) …….(ii)
∠FGH = 1/2m(arc FH) …….(iii)
Therefore, from equations (i), (ii), and (iii), we have:
m(arc EG) = m(arc FH)
Hence, proved.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 17 | Page 88
Click Here to see All the Textbook solution of Circle
