In the given figure, m(arc WY) = 44°, m(arc ZX) = 68°, then (1) Find the measure of ∠ ZTX.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 15 | Page 87
In the given figure, m(arc WY) = 44°, m(arc ZX) = 68°, then
(1) Find the measure of ∠ ZTX.
(2) If WT = 4.8, TX = 8.0,
YT = 6.4, find TZ.
(3) If WX = 25, YT = 8,
YZ = 26, find WT.
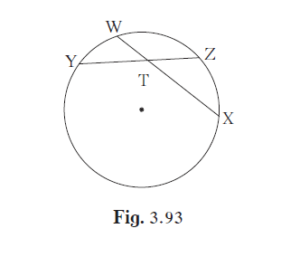
XW and YZ are two chords of a circle intersecting each other in the interior of the circle at T.
(1)
If two chords of a circle intersect each other in the interior of a circle then the measure of the angle between them is half the sum of measures of arcs intercepted by the angle and its opposite angle.
∴ ∠ZTX = `1/2`[m(arc ZX) + m(arc WY)] =`1/2 xx(68° + 44°) = 1/2 xx 112° = 56°`
Thus, the measure of ∠ZTX is 56º.
(2)
WT × TX = YT × TZ (Theorem of internal division of chords)
⇒ 4.8 × 8 = 6.4 × TZ
⇒ TZ =`(4.8xx8)/6.4 = 6`
(3)
WT × TX = YT × TZ (Theorem of internal division of chords)
⇒ WT × (WX − WT) = YT × (YZ − YT)
⇒ WT × (25 − WT) = 8 × (26 − 8)
⇒ 25WT − WT2 = 8 × 18 = 144
⇒ WT2 − 25WT + 144 = 0
⇒ WT2 − 16WT − 9WT + 144 = 0
⇒ WT(WT − 16) − 9(WT − 16) = 0
⇒ (WT − 16)(WT − 9) = 0
⇒ WT − 16 = 0 or WT − 9 = 0
⇒ WT = 16 or WT = 9
Explanation:-
Given: XW and YZ are two chords of a circle intersecting each other in the interior of the circle at T.
(1) By the theorem on the angle between two intersecting chords, if two chords of a circle intersect each other in the interior of a circle, then the measure of the angle between them is half the sum of measures of arcs intercepted by the angle and its opposite angle. Hence,
∠ZTX = 1/2[m(arc ZX) + m(arc WY)] = 1/2[68° + 44°] = 1/2×112° = 56°.
Thus, the measure of ∠ZTX is 56°.
(2) Using the theorem of internal division of chords, we have WT × TX = YT × TZ.
Substituting the given values, we get 4.8 × 8 = 6.4 × TZ.
Therefore, TZ = (4.8xx8)/6.4 = 6.
(3) Using the same theorem of internal division of chords, we have WT × (WX – WT) = YT × (YZ – YT).
Substituting the given values, we get WT × (25 – WT) = 8 × (26 – 8).
Simplifying the equation, we get:
WT<sup>2</sup> – 25WT + 144 = 0
This is a quadratic equation, which can be solved using the quadratic formula. The solutions are:
WT = 16 or WT = 9.
Therefore, WT is either 16 or 9.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 15 | Page 87
Click Here to see All the Textbook solution of Circle
