In the given figure, line PR touches the circle at point Q. Answer the following questions with the help of the figure. (1) What is the sum of ∠ TAQ and ∠ TSQ ? (2) Find the angles which are congruent to ∠ AQP.  (3) Which angles are congruent to ∠ QTS ? (4) ∠TAS = 65°, find the measure of ∠TQS and arc TS. (5) If ∠AQP = 42°and ∠SQR = 58° find measure of ∠ATS.

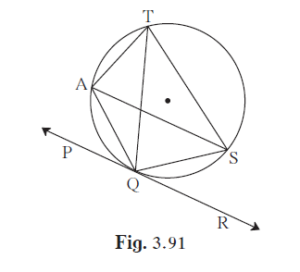
(1) As TAQS is a cyclic quadrilateral, ∠TAQ + ∠TSQ = 180° (Sum of opposite angles of a cyclic quadrilateral is 180°)

(2) ∠ASQ and ∠ATQ

(3) ∠ QAS and ∠SQR

(4) ∠TAS = 65° ∠ TQS = ∠ TAS = 65° (angle by same arc TS in the same sector) m(arc TS) = ∠TQS + ∠TAS ⇒ m(arc TS) = 65 + 65 = 130°

(5) ∠AQP + ∠AQS + ∠SQR = 180° ⇒ 42 + ∠AQS + 58 = 180 ⇒ ∠AQS + 100 = 180 ⇒ ∠AQS = 80 ∠ AQS + ∠ ATS = 180° (opposite angles of a cyclic quadrilateral) ⇒ 80 + ∠ATS = 180 ⇒ ∠ATS = 100°