In the figure, line l touches the circle with center O at point P.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 9 | Page 86
In the figure, line l touches the circle with center O at point P. Q is the midpoint of radius OP. RS is a chord through Q such that chords RS || line l. If RS = 12, find the radius of the circle.
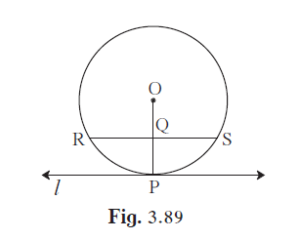
Let the radius of the circle be r.
line l is the tangent to the circle and
seg OP is the radius. ...[Given]
∴ seg OP ⊥ line l ...[Tangent theorem]
chord RS || line l ...[Given]
∴ seg OP ⊥ chord RS
∴ QS = `1/2` RS ...[Perpendicular drawn from the center of the circle to the chord bisects the chord]
∴ QS = `1/2 xx 12`
∴ QR = QS = 6 cm
Also,
OQ = `1/2` OP ......[Q is the midpoint of OP]
∴ OQ = `1/2` r
In ∆OQS,
∠OQS = 90° ....[seg OP ⊥ chord RS ]
∴ OS2 = OQ2 + QS2 ...[Pythagoras theorem]
∴ r2 = `(1/2 "r")^2 + 6^2`
∴ r2 = `1/4 "r"^2` + 36
∴ r2 - `1/4 "r"^2` = 36
∴ `3/4 "r"^2` = 36
∴ r2 = `(36 xx 4)/3`
∴ r2 = 48
∴ r = `sqrt(48)`
∴ r = `4sqrt(3)` cm ....[Taking square root of both sides]
∴ The radius of the given circle is `4sqrt(3)` cm.
Explanation:-
We are given a circle with radius r and a tangent line l that intersects the circle at point P. We are also given a chord RS that is parallel to line l. We need to find the radius of the circle.
We start by using the tangent theorem, which tells us that a line tangent to a circle is perpendicular to the radius at the point of contact. Therefore, we have seg OP perpendicular to line l.
Since chord RS is parallel to line l, we can use the perpendicular bisector theorem to find that QS = 1/2 RS. This is because the perpendicular drawn from the center of the circle to a chord bisects the chord.
We are also given that RS = 12 cm, so QS = 1/2 * 12 = 6 cm. Therefore, QR = QS = 6 cm.
Next, we use the fact that Q is the midpoint of OP to find that OQ = 1/2 OP. Since we know that seg OP has length r, we have OQ = 1/2 r.
Now, we can use the Pythagorean theorem in triangle OQS to relate the sides OQ, QS, and OS. Since seg OP is perpendicular to chord RS, angle OQS is a right angle. Therefore, we have:
OS^2 = OQ^2 + QS^2
Substituting OQ = 1/2 r and QS = 6, we get:
r^2/4 = OS^2 – 36
We also know that the radius of the circle is r, so we can substitute r^2 for OS^2 to get:
r^2/4 = r^2 – 36
Multiplying both sides by 4 gives:
r^2 = 4r^2 – 144
Simplifying, we get:
3r^2 = 144
Dividing both sides by 3 gives:
r^2 = 48
Taking the square root of both sides, we get:
r = 4 sqrt(3)
Therefore, the radius of the circle is 4 sqrt(3) cm.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 9 | Page 86
Click Here to see All the Textbook solution of Circle
