In the adjoining figure circles with centres X and Y touch each other at point Z
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 7 | Page 85
In the adjoining figure circles with centres X and Y touch each other at point Z. A secant passing through Z intersects the circles at points A and B respectively. Prove that, radius XA || radius YB. Fill in the blanks and complete the proof.
Construction: Draw segments XZ and YZ.
Proof:
By theorem of touching circles, points X, Z, Y are `square`.
∴ ∠XZA ≅ `square` …(opposite angles)
Let ∠XZA = ∠BZY = a …(I)
Now, seg XA ≅ seg XZ …[Radii of the same circle]
∴∠XAZ = `square` = a …[isosceles triangle theorem](II)
Similarly,
seg YB ≅ seg YZ …[Radii of the same circle]
∴∠BZY = `square` = a …[isosceles triangle theorem](III)
∴ from (I), (II), (III),
∠XAZ = `square`
∴ radius XA || radius YZ …[`square`]
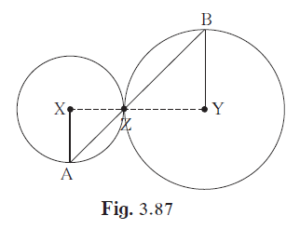
Construction: Draw segments XZ and YZ.
Proof:
By theorem of touching circles, points X, Z, Y are collinear.
∴ ∠XZA ≅ ∠BZY ...(opposite angles)
Let ∠XZA = ∠BZY = a .....(I)
Now, seg XA ≅ seg XZ ...[Radii of the same circle]
∴∠XAZ = ∠XZA = a ....[isosceles triangle theorem](II)
Similarly, seg YB ≅ seg YZ ....[Radii of the same circle]
∴∠BZY = ∠ZBY = a ...[isosceles triangle theorem](III)
∴ from (I), (II), (III),
∠XAZ = ∠ZBY
∴ radius XA || radius YB ...[Alternate angle test]
Explanation:-
The given construction is to draw segments XZ and YZ. The proof is as follows:
By the theorem of touching circles, since the circles with centers A and B touch at point Z, and X and Y are the points of contact of the circles with the line of centers, therefore points X, Z, and Y are collinear.
Thus, we have angle XZA congruent to angle BZY (opposite angles).
Let angle XZA = angle BZY = a.
Now, XA is congruent to XZ and YB is congruent to YZ, since they are radii of the same circles.
Therefore, angle XAZ = angle XZA = a (isosceles triangle theorem).
Similarly, angle BZY = angle ZBY = a (isosceles triangle theorem).
Therefore, from (I), (II), (III), we have angle XAZ = angle ZBY.
Therefore, radius XA is parallel to radius YB (alternate angle test).
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 7 | Page 85
Click Here to see All the Textbook solution of Circle
