In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 5 | Page 85
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.
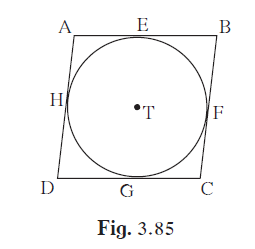
ABCD is a parallelogram.
∴ AB = CD .....(1) (Opposite sides of parallelogram are equal)
AD = BC .....(2) (Opposite sides of parallelogram are equal)
Tangent segments drawn from an external point to a circle are congruent.
AE = AH .....(3)
DG = DH .....(4)
BE = BF .....(5)
CG = CF .....(6)
Adding (3), (4), (5) and (6), we get
AE + BE + CG + DG = AH + DH + BF + CF
⇒ AB + CD = AD + BC .....(7)
From (1), (2) and (7), we have
2AB = 2AD
⇒ AB = AD
∴ AD = AB = AE + EB = 4.5 + 5.5 = 10 units
Explanation:-
The given problem involves a parallelogram ABCD, where tangent segments are drawn from an external point to a circle. The aim is to find the value of AD, which is one of the sides of the parallelogram.
Given information:
- AB = CD (opposite sides of parallelogram are equal) …(1)
- AD = BC (opposite sides of parallelogram are equal) …(2)
- AE = AH, DG = DH, BE = BF, CG = CF (tangent segments drawn from an external point to a circle are congruent)
- Adding (3), (4), (5), and (6), we get: AE + BE + CG + DG = AH + DH + BF + CF AB + CD = AD + BC …(7)
Using equations (1), (2), and (7), we can write: 2AB = 2AD AB = AD
Therefore, we can conclude that AD is equal to AB, which is also equal to AE + EB. We are given that AE = 4.5 and EB = 5.5. Hence, AD = AB = AE + EB = 4.5 + 5.5 = 10 units.
Thus, the value of AD is 10 units.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 5 | Page 84
Click Here to see All the Textbook solution of Circle
