In the given figure, M is the centre of the circle and seg KL is a tangent segment.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 3 | Page 84
In the given figure, M is the centre of the circle and seg KL is a tangent segment.
If MK = 12, KL = \[6\sqrt{3}\] then find –
(1) Radius of the circle.
(2) Measures of ∠K and ∠M.
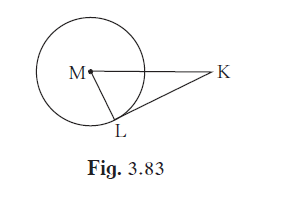
(1) The tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ ∠MLK = 90º
In right ∆MLK,
\[{MK}^2 = {ML}^2 + {LK}^2 \]
\[ \Rightarrow ML = \sqrt{{MK}^2 - {LK}^2}\]
\[ \Rightarrow ML = \sqrt{\left( 12 \right)^2 - \left( 6\sqrt{3} \right)^2}\]
\[ \Rightarrow ML = \sqrt{144 - 108}\]
\[ \Rightarrow ML = \sqrt{36} = 6 \] cm
Thus, the radius of the circle is 6 cm.
(2) In right ∆MLK,
\[\tan\angle K = \frac{ML}{KL}\]
\[ \Rightarrow \tan\angle K = \frac{6}{6\sqrt{3}} = \frac{1}{\sqrt{3}}\]
\[ \Rightarrow \tan\angle K = \tan30°\]
\[ \Rightarrow \angle K = 30°\]
Using angle sum property, we have
\[\angle K + \angle L + \angle M = 180^\circ\]
\[ \Rightarrow 30^\circ + 90^\circ + \angle M = 180^\circ\]
\[ \Rightarrow 120^\circ + \angle M = 180^\circ\]
\[ \Rightarrow \angle M = 180^\circ - 120^\circ = 60^\circ\]
Thus, the measures of ∠K and ∠M are 30º and 60º, respectively.
Explanation:-
The given problem involves finding the radius and angles of a circle, given certain geometric properties. The solution is as follows:
(1) Using the property that the tangent at any point of a circle is perpendicular to the radius through the point of contact, we know that angle MLK is 90 degrees. We can then use the Pythagorean theorem in right triangle MLK to find the length of ML, which is the radius of the circle. This gives us:
MK^2 = ML^2 + LK^2 ML = sqrt(MK^2 – LK^2) ML = sqrt(12^2 – (6sqrt(3))^2) ML = sqrt(144 – 108) ML = sqrt(36) = 6 cm
Therefore, the radius of the circle is 6 cm.
(2) Using right triangle MLK, we can find the measure of angle K by taking the tangent of angle K, which is opposite over adjacent. This gives us:
tan(K) = ML/KL tan(K) = 6/(6sqrt(3)) tan(K) = 1/sqrt(3) tan(K) = tan(30 degrees) K = 30 degrees
Using the angle sum property for triangles, we know that the sum of the angles in triangle MLK is 180 degrees. We can then solve for angle M by subtracting angles K and L from 180 degrees. This gives us:
K + L + M = 180 degrees 30 + 90 + M = 180 120 + M = 180 M = 180 – 120 = 60 degrees
Therefore, the measures of angles K and M are 30 degrees and 60 degrees, respectively.
Chapter 3 – Circle – Text Book Solution
Problem Set 3 | Q 3 | Page 84
Click Here to see All the Textbook solution of Circle
