In the given figure, seg EF is a dia meter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE × GE = 4r2
Chapter 3 – Circle – Text Book Solution
Practice Set 3.5 | Q 5 | Page 82
In the given figure, seg EF is a dia meter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE × GE = 4r2
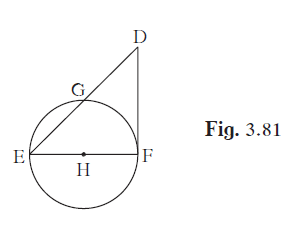
In the given figure, seg EF is a diameter and seg DF is a tangent segment.
∴ ∠HFD = 90º (Tangent at any point of a circle is perpendicular to the radius through the point of contact)
In right ∆DEF,
DE2 = EF2 + DF2 .....(1)
Using tangent secant segments theorem, we have
DE × DG = DF2 .....(2)
Subtracting (2) from (1), we get
DE2 − DE × DG = EF2 + DF2 − DF2
⇒ DE × (DE − DG) = EF2
⇒ DE × GE = (2r)2 = 4r2 (EF = 2r)
Hence, DE × GE = 4r2
Explanation:-
In the given figure, seg EF is a diameter and seg DF is a tangent segment, so we know that ∠HFD = 90° since the tangent at any point of a circle is perpendicular to the radius through the point of contact.
In right ∆DEF, we can use the Pythagorean theorem to get:
DE^2 = EF^2 + DF^2 ……….(1)
Using the tangent secant segments theorem, we have:
DE × DG = DF^2 ………..(2)
Subtracting equation (2) from equation (1), we get:
DE^2 – DE × DG = EF^2 + DF^2 – DF^2
Simplifying, we get:
DE × (DE – DG) = EF^2
Since EF is a diameter of the circle, we know that EF = 2r, where r is the radius of the circle. Substituting this into the equation, we get:
DE × (DE – DG) = (2r)^2 = 4r^2
Therefore, we can conclude that DE × GE = 4r^2.
Chapter 3 – Circle – Text Book Solution
Practice set 3.5 | Q 5 | Page 82
Click Here to see All the Textbook solution of Circle
